Limite finito di una funzione per x che tende all'infinito

Consideriamo la seguente funzione:

Sappiamo che essa definita per tutti i valori di ( x
e 0 ), quindi la funzione sicuramente definita per valori di x molto grandi o molto piccoli, cio in un intorno di infinito.

Esaminiamo, quindi, il comportamento della funzione per valori di x positivi sempre pi grandi, e per valori di x negativi, sempre pi grandi in valore assoluto. Riassumiamo in una tabella i risultati ottenuti:

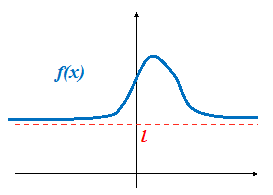
Notiamo quindi che a mano a mano che i valori di x crescono, la funzione si avvicina sempre di pi a 1, e si dice che per x tendente all'infinito, f(x) ha per limite 1, o anche f(x) tende a 1 per x tendente all'infinito.

Possiamo quindi affermare che, per valori di x abbastanza grandi, in valore assoluto, la distanza di f(x) da 1 sempre pi piccola, possiamo dire che il

valore di

può essere reso piccolo a piacere, cioè minore di qualsiasi numero positivo arbitrariamente piccolo.

Esprimiamo questo concetto con una definizione formale:

Definizione di limite all'infinito

Si dice che, per x tendente all'infinito, la funzione y = f(x) ha per limite l, e si scrive:

se, comunque si scelga un numero positivo ?, arbitrariamente piccolo, si può determinare, in corrispondenza di esso, un intorno di infinito tale che, per ogni x appartenente a tale intorno, si ha:

In particolare, con la scrittura

intendiamo i valori di x che tendono a

e a

.

In questo caso, per verificare la correttezza di un limite, dobbiamo accertarci che la disequazione

abbia come insieme delle soluzioni un intorno di infinito.

Vediamo un esempio:

Esempio di limite all'infinito

Verifichiamo il seguente limite:

Dobbiamo verificare che per valori di x sempre pi grandi, o per valori di x sempre pi piccoli, la funzione si avvicini sempre di pi al valore 1.

Quindi, sappiamo che la differenza tra la funzione stessa e il valore 1 diventerà piccola a piacere, per questi valori di x, e in particolare, sarà sicuramente pi piccola di un numero arbitrario ?; impostiamo quindi, la seguente disequazione:

Risolviamo la disequazione:

Poiché al numeratore abbiamo un valore numerico, possiamo separare i valori assoluti, e girare la frazione, ricordandoci di cambiare il verso della disequazione:

Da cui otteniamo:

Risolviamo le due disequazioni, ricordandoci che le soluzioni finali saranno l'unione delle soluzioni delle singole disequazioni:

Possiamo rappresentare l'insieme delle soluzioni anche con un'altra notazione:

Il risultato ottenuto un intorno di infinito, quindi concludiamo affermando che il limite verificato.

Casi particolari

Con la notazione

, se non specifichiamo il segno di infinito, intendiamo infinito generico, cioè sia

che

.

In alcuni casi, per, ci si pu riferire solo a valori molto grandi positivi di x, o solo a valori molto piccoli negativi di x.

Vediamo quindi le due seguenti definizioni:

Definizione di limite per x che tende a pi infinito

Si dice che, per x tendente a

, la funzione f(x) ha limite l, e si scrive:

se, comunque fissato un numero positivo

, arbitrariamente piccolo, si può determinare, in corrispondenza ad esso, un intorno di

tale che, per ogni x di tale intorno, si ha che:

Definizione di limite a meno infinito

Si dice che, per x tendente a

, la funzione f(x) ha limite l, e si scrive:

se, comunque scelto un numero positivo

, arbitrariamente piccolo, si può determinare, in corrispondenza ad esso, un intorno di

tale che, per ogni x di tale intorno, si ha che:

Asintoti orizzontali

Come abbiamo detto prima, se il limite per

per una funzione f(x), vale l, sappiamo che la funzione, per valori sempre pi grandi di x, si avvicinerà sempre di pi alla retta di equazione y = l. Si dice, in questo caso, che la funzione ha un asintoto orizzontale destro.

Allo stesso modo, se per

il limite della funzione vale l, diremo che la funzione ha un asintoto orizzontale sinistro di equazione y = l.

In particolare, se non si specifica il segno di

, la funzione avrà un asintoto orizzontale sia destro che sinistro.

Riassumiamo i vari casi possibili: