Funzioni esponenziali spiegazione generale

Funzioni esponenziali

La forma generale di una funzione esponenziale è f(x) = a^x, dove "a" è una costante positiva diversa da 1 e "x" è la variabile indipendente. Questa forma è conosciuta come esponenziale di base "a".

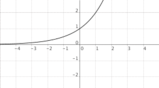
Se la base "a" è maggiore di 1, la funzione esponenziale mostra una crescita esponenziale. Ad esempio, se a = 2, allora la funzione f(x) = 2^x avrà un aumento rapido dei valori per valori crescenti di "x". Ogni volta che "x" aumenta di 1, il valore della funzione raddoppia. Questo tipo di crescita è comune in situazioni come il raddoppio del numero di batteri in una cultura o l'aumento del valore di un investimento a interesse composto.

D'altra parte, se la base "a" è compresa tra 0 e 1, la funzione esponenziale mostra un decadimento esponenziale. Ad esempio, se a = 1/2, allora la funzione f(x) = (1/2)^x diminuisce rapidamente per valori crescenti di "x". Ogni volta che "x" aumenta di 1, il valore della funzione si dimezza. Questo tipo di decadimento è spesso osservato in situazioni come la radioattività o il decadimento di una sostanza chimica nel tempo.

Le funzioni esponenziali hanno diverse proprietà importanti. Una di queste è la proprietà di simmetria rispetto all'asse delle ordinate. Ciò significa che se sostituisci "x" con "-x" nell'equazione, ottieni lo stesso valore della funzione. Questa simmetria riflette il fatto che le funzioni esponenziali possono crescere rapidamente sia verso l'alto che verso il basso.

Un'altra proprietà fondamentale è la regola degli esponenti, che stabilisce che a^x * a^y = a^(x+y). Questa regola ci permette di semplificare i calcoli con le funzioni esponenziali e di combinare termini con la stessa base. Ad esempio, 2^3 * 2^4 = 2^(3+4) = 2^7.

Le funzioni esponenziali sono spesso utilizzate per modellare fenomeni reali in cui il tasso di crescita o di decadimento è proporzionale alla quantità presente. Ad esempio, nella crescita di una popolazione, la velocità di crescita è proporzionale al numero di individui presenti. Questo tipo di modelli può essere descritto da equazioni differenziali esponenziali, che coinvolgono derivate di funzioni esponenziali.

Le funzioni esponenziali sono anche strettamente legate alla funzione esponenziale naturale, che ha come base il numero di Eulero "e" (circa 2,71828). La funzione esponenziale naturale è indicata con "exp(x)" o "e^x" e ha numerose applicazioni in matematica, fisica e ingegneria.

In conclusione, le funzioni esponenziali sono un potente strumento matematico per descrivere fenomeni che crescono o decadono in modo esponenziale nel tempo. Sono caratterizzate da una base positiva diversa da 1 e mostrano proprietà di crescita o decadimento rapido. Le funzioni esponenziali sono ampiamente utilizzate in vari campi per modellare fenomeni reali e semplificare i calcoli matematici.