Definizione di limite di una funzione

Sia y = f(x) una funzione definita in un insieme E e sia  x₀ un punto di accumulazione per E (x₀ può anche non essere contenuto in E).

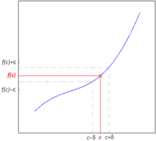
Definizione 1: la funzione f(x) si dice convergente nel punto  x₀ su  E  se  esiste  un numero reale l che  gode  della  seguente proprietà: scelto a piacere un numero reale ε > 0, si può sempre trovare in corrispondenza un intorno I(x₀,δ) di x₀ dipendente da ε tale che, per tutti gli x di E diversi da x₀ e contenuti nell'intorno I, risulti:

Ciò si esprime simbolicamente scrivendo:

Cosa vuol dire in parole povere? Che lungo la funzione, avvicinandosi ad x₀ lungo le ascisse, ci avviciniamo anche al valore l lungo le
ordinate.

La definizione funziona come una scommessa: "scommettiamo che
riesco a stare vicinissimo a l, allontanandomi al massimo di
1/1000?" e così fisso ε = 1/1000. Vinco la scommessa, perché
esiste un intorno I in cui riesco a stare più vicino di ε.

Esempio: consideriamo la funzione y = x² definita in R; si ha .

Infatti, scelto a piacere un ε > 0 risulta
sse ,
che è appunto un intorno di 0.

Definizione 2: la funzione f(x) si
dice divergente positivamente (risp. negativamente) nel punto  x₀ su  E  se
scelto a piacere un numero reale k > 0, si può sempre trovare in
corrispondenza un intorno I(x₀,δ) di x₀
dipendente da k tale che, per tutti gli x di E diversi da x₀
e contenuti nell'intorno I, risulti:

Ciò si esprime simbolicamente scrivendo:

Esempio: consideriamo la funzione definita in R \ {0}. Si ha .

Infatti, scelto a piacere un k > 0 risulta
sse ,
che è un intorno di 0 da cui è stato escluso 0.

Definizione 3: la funzione f(x) si
dice convergente a + ∞
 (risp. - ∞)
su  E  se  esiste  un
numero reale l che  gode  della  seguente proprietà:
scelto a piacere un numero reale ε > 0, si può sempre trovare in
corrispondenza un intervallo illimitato I = (k,+ ∞)
(risp.(-∞,-k)) dipendente da ε
tale che, per tutti gli x di E contenuti
nell'intervallo I, risulti:

Ciò si esprime simbolicamente scrivendo:

Esempio: consideriamo ancora  la funzione definita in R \ {0}. Si ha .

Infatti, scelto a piacere un k > 0 risulta
se ,
che è un intorno di + ∞.

Definizione 4: la funzione f(x) si
dice divergente positivamente (risp. negativamente) a +∞ su  E  se  scelto a piacere un numero reale k > 0, si può sempre trovare in
corrispondenza un intervallo illimitato I = (h,+∞)
dipendente da k tale che, per tutti gli x di E
contenuti nell'intervallo I, risulti:

Ciò si esprime simbolicamente scrivendo:

Analogamente per ,
con un intervallo I = (- ∞,-h).

Esempio: consideriamo la funzione y = x² definita in R. Si ha .

Infatti, scelto a piacere un k > 0 risulta x² > k sse ,
che è un intorno di + ∞.

Vi sono anche funzioni che non hanno limite per o
per .
Tali funzioni si dicono indeterminate o oscillanti nel punto x₀ (±∞).
Ad esempio,
è indeterminata nel punto 0, mentre sin x è indeterminata a ±∞,
in quanto avvicinandosi a tali valori la funzione non si stabilizza verso un
unico valore.