[math]\begin{cases} x^2-7x>0 \\ x^2+x>7x-10 \ \end{cases}[/math]
[math]\begin{cases} x^2-7x>0 \\ x^2+x>7x-10 \ \end{cases}[/math]
;
[math]\begin{cases} x(x-7)>0 \\ x^2-6x+10>0 \ \end{cases}[/math]
;
Studiamo le due disequazioni singolarmente
1)
[math]x(x-7)>0 \Rightarrow x>0 \wedge x-7>0[/math]
, cioè la soluzione sarà:
[math]x>0 \vee x>7[/math]
2)
[math]x^2-6x+10>0[/math]
[math]\frac{\Delta}{4}=(\frac{b}{2})^2-ac=(-3)^2-(10 \cdot 1)=9-10=-1>0[/math]
Quindi la disequazione non ammette soluzioni reali.
Pertanto
[math]\begin{cases} x>0 \vee x>7 \\ \Phi \ \end{cases}[/math]
;Soluzione del sistema sarà l'intersezione delle singole soluzioni delle disequazioni che lo compongono.
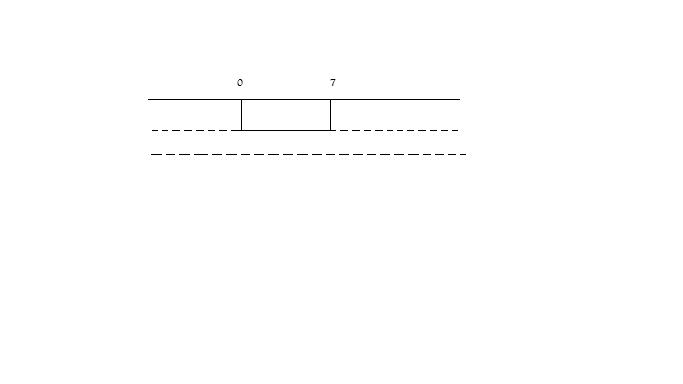
Quindi la soluzione sarà:
[math]\Phi[/math]
.
![Disequazioni: [math]{2}\cdot{5}^{x}+{4}\cdot{5}^{{{3}-{x}}}\lt{205}[/math]](https://cdn.skuola.net/shared/thumb/159x141/news_foto/2017/10/dis_esp_e01.jpg)
![Disequazioni: [math] {\left|\frac{{{2}{x}+{5}}}{{{4}{x}-{2}}}-\frac{{{x}-{1}}}{{{1}-{2}{x}}}\right|}\lt\frac{2}{{3}} [/math]](https://cdn.skuola.net/shared/thumb/159x141/news_foto/2017/10/dise_e2-615x724.jpg)
Accedi a tutti gli appunti
Tutor AI: studia meglio e in meno tempo
