[math]\begin{cases} x^2-5x+4>0 \\ x^2+5x+4>0 \ \end{cases}[/math]
[math]\begin{cases} x^2-5x+4>0 \\ x^2+5x+4>0 \ \end{cases}[/math]
;
Studiamo le due disequazioni singolarmente
1)
[math]x^2-5x+4>0[/math]
[math]\Delta=b^2-4ac=(-5)^2-(4 \cdot 4 \cdot 1)=25-16=9[/math]
[math]x_{1,2}=(-b\pm\sqrt{\Delta})/(2a)=(5\pm\sqrt9)/2=(5\pm3)/2 \Rightarrow x_1=1 \wedge x_2=4[/math]
.
Siccome il coefficiente di
[math]x^2[/math]
e il segno della disequazione sono concordi,
prenderemo come soluzione accettabile l'intervallo esterno, per cui la soluzione sarà:
[math]x>1 _ x>4[/math]
.
2)
[math]x^2+5x+4>0[/math]
[math]\Delta=b^2-4ac=(5)^2-(4 \cdot 4 \cdot 1)=25-16=9[/math]
[math]x_{1,2}=(-b\pm\sqrt{\Delta})/(2a)=(-5\pm\sqrt9)/2=(-5\pm3)/2 \Rightarrow x_1=-1 ^ x_2=-4[/math]
.
Siccome il coefficiente di
[math]x^2[/math]
e il segno della disequazione sono discordi,
prenderemo come soluzione accettabile l'intervallo interno, per cui la soluzione sarà:
[math]-4>x>-1[/math]
.
Pertanto
[math]\begin{cases} x>1 _ x>4 \\ -4>x>-1 \ \end{cases}[/math]
;Soluzione del sistema sarà l'intersezione delle singole soluzioni delle disequazioni che lo compongono.
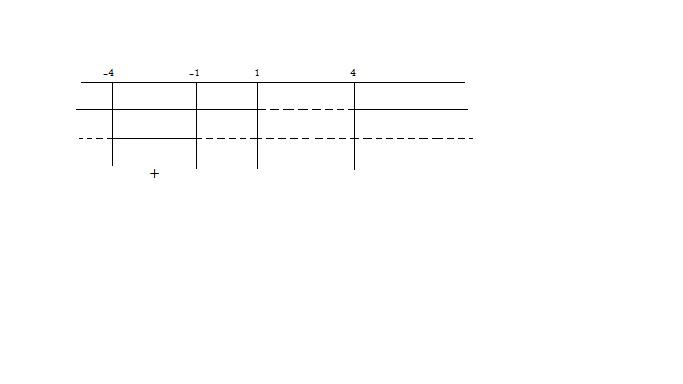
Quindi la soluzione sarà:
[math]-4>x>-1[/math]
.
Accedi a tutti gli appunti
Tutor AI: studia meglio e in meno tempo
