Sistema di tre disequazioni di secondo grado

Oggi risolveremo un semplice sistema di tre disequazioni di secondo grado. Il sistema è il seguente:

Cominciamo immediatamente a risolvere la prima, che è la seguente:

Consideriamo l'equazione associata che è la seguente:

Per determinare le due

, quindi, si utilizza la formula che ben conoscete:

Visto che questa disequazione mostra il segno maggiore, il risultato sarà composto da tutti i valori esterni a

e

, quindi i valori che risolvono questa disequazione sono i seguenti: (Non dobbiamo considerare gli estremi perché nella disequazione non compare il segno di

)

Bene, andiamo avanti e risolviamo la seconda, che voglio ricordavi che è:

Per quanto riguarda questa disequazione possiamo fare un'osservazione: possiamo notare che al primo membro compare un quadrato perfetto di binomio, infatti tutto ciò può essere scritto come:

Ma noi sappiamo che un quadrato è sempre maggiore o uguale di

, quindi questa disequazione è verificata per:

Possiamo quindi passare direttamente alla terza, riscriviamola:

In questo caso consideriamo l'equazione associata:

E risolviamola molto semplicemente, determinando come

i seguenti:

Il risultato di questa disequazione prevede che si prendano tutti i valori esterni a

e

.

Quindi il grafico sarà il seguente:

A questo punto, visto che noi non dimentichiamo che dobbiamo risolvere il sistema, dobbiamo considerare contemporaneamente le soluzioni comuni. Quindi vediamo:

--> La prima disequazione è risolta per i valori esterni a

e

. (In nero)

--> La seconda disequazione è risolta per ogni

(In blu)

--> La terza disequazione, che considera i valori esterni a

ed

esclusi

ed

(In verde), ci permette di concludere il nostro grafico:

A questo punto non ci resta che prendere i valori comuni a tutte e tre le soluzioni per risolvere il nostro sistema. I valori comuni sono logicamente: (In rosso)

Possiamo quindi, infine, scrivere le soluzioni che sono le seguenti:

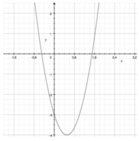
Come dimostrato dal grafico.