Risoluzione delle disequazioni

Ominide

7 min. di lettura

Vota

Indice

Risoluzione di una disequazione lineare
Risoluzione grafica delle disequazioni lineari

Risoluzione di una disequazione lineare

Vediamo alcuni passaggi che ci aiuteranno nella risoluzione delle disequazioni lineari, cioè di primo grado, nell'incognita x:

Per prima cosa, si eseguono le eventuali operazioni, semplificando la scrittura, e si eliminano i denominatori delle eventuali frazioni;
Si trasportano tutti i termini contenenti l'incognita al primo membro e tutti i fattori numerici al secondo membro;
si svolgono i conti, semplificando gli eventuali termini simili;
A questo punto, la disuguaglianza si presenter in una delle quattro forme seguenti:
[math] \displaystyle ax \gt b[/math]
;
[math] \displaystyle ax \lt b[/math]
;
[math] \displaystyle ax \le b[/math]
;
[math] \displaystyle ax \ge b[/math]
; distinguiamo due casi:
- Se
  [math] \displaystyle a \ne 0[/math]
  si dividono entrambi i membri della disequazione per a, tenendo conto del suo segno: se a è negativo, dobbiamo cambiare il verso delle disequazione;
- Se a = 0, il primo membro assume il valore 0 qualunque sia il valore di x. In base al valore di b la disequazione si trasformer in una disuguaglianza sempre vera o sempre falsa; di conseguenza, avremmo una disequazione verificata per ogni x
  (l'insieme delle soluzioni R) oppure una disequazione mai verificata (l'insieme delle soluzioni l'insieme vuoto);

Esempio: risolviamo la seguente disequazione:

[math] \displaystyle \frac{2(1+2x)}{5} - \frac{2x+3}{4} - \frac{1}{5} \lt \frac{3}{10}x + 1[/math]

cominciamo riducendo le frazioni al denominatore comune, e sommando le frazioni:

[math] \displaystyle \frac{4 \cdot 2 (1+2x) - 5\cdot(2x+3)-4}{20} \lt \frac{2\cdot 3x + 20}{20}[/math]

dato che il denominatore positivo, possiamo eliminarlo, ottenendo sempre una disequazione equivalente:

[math] \displaystyle 4 \cdot 2(1+2x) - 5 \cdot (2x+3) - 4 \lt 2 \cdot 3x + 20[/math]

svolgiamo i calcoli, portando tutti i termini con l'incognita al primo membro, e tutti numeri al secondo membro:

[math] \displaystyle 8 + 16x - 10x - 15 - 4 \lt 6x + 20[/math]

[math] \displaystyle 16x - 10x - 6x \lt 20 - 8 + 15 + 4[/math]

La disequazione ottenuta si trasforma in una disuguaglianza vera (

[math] \displaystyle 0 \lt 31[/math]

), qualunque sia il valore di x; concludiamo che la disequazione sempre verificata, e scriviamo:

[math] \displaystyle S = \mathbb{R} [/math]

Esempio: risolviamo la seguente disequazione:

[math] \displaystyle (x+2)^2 - 2x \lt x^2 - 4x - 3[/math]

svolgiamo il quadrato del binomio:

[math] \displaystyle x^2 + 4 + 4x - 2x \lt x^2 - 4x - 3[/math]

notiamo che in entrambi i membri compare il termine x alla seconda, che possiamo eliminare:

[math] \displaystyle 4 + 4x - 2x \lt -4x - 3[/math]

trasportiamo i termini contenenti l'incognita al primo membro, e i numeri al secondo, poi sommiamo i termini simili:

[math] \displaystyle 4x - 2x + 4x \lt -3 - 4[/math]

[math] \displaystyle 6x \lt -7[/math]

dividiamo entrambi i membri per il coefficiente di x:

[math] \displaystyle \frac{6x}{6} \lt \frac{-7}{6}[/math]

[math] \displaystyle x \lt -\frac{7}{6}[/math]

Possiamo anche scrivere linsieme delle soluzioni in questo modo:

[math] \displaystyle S = \Big( -\infty; -\frac{7}{6} \Big)[/math]

Risoluzione grafica delle disequazioni lineari

Consideriamo una disequazione ridotta in forma normale, come si presenta, cio, dopo i passaggi si semplificazione;

supponiamo di avere una disequazione del tipo
[math] \displaystyle ax \lt b [/math]
, cioè
[math] \displaystyle ax - b \lt 0[/math]
.

Osserviamo che il suo primo membro può essere considerato come lespressione analitica di una funzione lineare, e precisamente della funzione di equazione

[math] \displaystyle y = ax - b[/math]

, l'equazione di una retta.

Per risolvere graficamente una disequazione di questo tipo, dobbiamo considerare i punti della retta di equazione

[math] y = ax - b [/math]

che si trovano al di sotto dell'asse x, poich per questi punti si ha

[math] \displaystyle y \lt 0[/math]

Linsieme delle soluzioni dato dallinsieme di tutti questi punti.

Esempio: consideriamo la disequazione

[math] \displaystyle 2x + 1 \lt 0[/math]

l'equazione della retta che dovremmo rappresentare

[math] \displaystyle y = 2x + 1[/math]

per tracciare il grafico della retta, diamo ad x vedi valori arbitrari, trovando i corrispettivi valori di y:

[math] \displaystyle x = 0 \rightarrow y = 1[/math]

[math] \displaystyle x = 1 \rightarrow y = 2 + 1 = 3[/math]

sapendo che la retta passa per i punti (0 ; 1) e (1 ; 3), possiamo rappresentarla

nel piano cartesiano:

La soluzioni della disequazione è l'insieme dei numeri per cui la retta assume valori negativi, cioè si trova al di sotto dell'asse delle ascisse; il punto in cui la retta interseca l'asse x si può trovare ponendo y = 0:

[math] \begin{cases} y = 0 \\ y = 2x + 1 \end{cases} \rightarrow \begin{cases} y = 0 \\ x = -\frac{1}{2} \end{cases} [/math]

Il punto di intersezione è quindi (- 1/2 ; 0) per valori minori di x la retta si trova al di sotto dell'asse x; quindi, l'insieme delle soluzioni è dato da:

[math] \displaystyle S = \Big(-\infty; -\frac{1}{2} \Big)[/math]

supponiamo ora di avere una disequazione del tipo
[math] \displaystyle ax \gt b [/math]
, cioè
[math] \displaystyle ax - b \gt 0 [/math]
.

Questa volta, dobbiamo considerare i punti della retta di equazione

[math] \displaystyle y = ax - b[/math]

che si trovano al di sopra dell'asse x, poiché per questi punti si ha

[math] \displaystyle y \gt 0 [/math]

. L'insieme delle soluzioni è dato dall'insieme di tutti questi punti.

Esempio: consideriamo la disequazione

[math] \displaystyle -\frac{1}{2}x + 4 \gt 0[/math]

l'equazione della retta che dovremmo rappresentare è

[math] \displaystyle y = -\frac{1}{2}x + 4[/math]

per tracciare il grafico della retta, diamo ad x vedi valori arbitrari, trovando i corrispettivi valori di y:

[math] \displaystyle x = 0 \rightarrow y = 4[/math]

[math] \displaystyle x = 2 \rightarrow y = -1 + 4 = 3[/math]

sapendo che la retta passa per i punti (0 ; 4) e (2 ; 3),tracciamo il suo grafico:

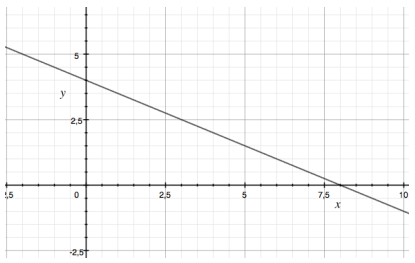
Risoluzione delle disequazioni articolo

La soluzioni della disequazione è l'insieme dei valori per cui la retta assume valori positivi, cioè si trova al di sopra dell'asse delle ascisse; il punto in cui la retta interseca l'asse x si può trovare ponendo y = 0:

[math] \begin{cases} y = 0 \\ y = -\frac{1}{2}x + 4 \end{cases} \rightarrow \begin{cases} y = 0 \\ x = 8 \end{cases} [/math]

Il punto di intersezione è quindi (8 ; 0); per valori minori di x la retta si trova al di sopra dell'asse x; quindi, l'insieme delle soluzioni è dato da:

[math] \displaystyle S = (-\infty; 8)[/math]

Risoluzione delle disequazioni