La somma delle misure del cateto maggiore e dell'ipotenusa di un triangolo rettangolo è
[math]9,8m[/math]
,
mentre la loro differenza è di
[math]0,2m[/math]
.
Calcola il perimetro e l'area del triangolo.
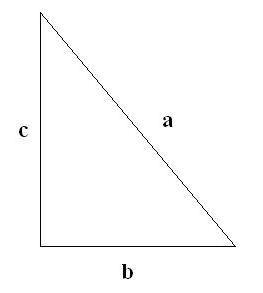Dati [math]a+c=9,8m[/math]
[math]a-c=0,2m[/math]
Svolgimento
L'ipotenusa, quindi, è più lunga del cateto maggiore di
[math]0,2m[/math]
.
Se dalla somma sottraiamo la differenza si ha:
[math](a+c)-(a-c)=2c[/math]
Sostituendo
[math](a+c)-(a-c)=(9,8-0,2)m=9,6=2c => c=(9,6)/2m=4,8m[/math]
quindi
[math]a=c+0,2m=(4,8+0,2)m=5m[/math]
Per il Teorema di Pitagora
[math]b=\sqrt{(a)^2-(c)^2}=\sqrt((5m)^2-(4,8m)^2)=\sqrt(25-23,04)m=\sqrt(1,96)m=1,4m[/math]
Pertanto
[math]2p=a+b+c=(5+1,4+4,8)m=11,2m[/math]
[math]A=(b \cdot c)/2=((1,4) \cdot (4,8))/2m^2=3,36m^2[/math]
.
Accedi a tutti gli appunti
Tutor AI: studia meglio e in meno tempo
