Indice
La correlazione
Nel caso in cui, considerate due distribuzioni X e Y, esista tra di loro una corrispondenza lineare, stabilita per mezzo di rette di regressione, è possibile dare una misura sintetica di tale corrispondenza.
Per fare questo, si utilizzano dei coefficienti, e tra i più usati troviamo il coefficiente di correlazione lineare di Bravais-Pearson, che si ottiene dal rapporto della covarianza delle distribuzioni per il prodotto delle loro deviazioni standard (cioè i loro scarti quadratici medi):
Il valore di tale indice è un numero reale compreso tra -1 e 1.
In particolare, possiamo notare che il coefficiente assume:
- il valore -1 nel caso di perfetta correlazione negativa;
- il valore 1 nel caso di perfetta correlazione positiva;
- il valore 0 se non vi è correlazione tra le distribuzioni;
- valori positivi nel caso di correlazione positiva;
- valori negativi nel caso di correlazione negativa.
Tra la correlazione e la regressione esiste un legame molto stretto, espresso dalla seguente:
dove i coefficienti
e
sono, rispettivamente, i coefficienti di regressione di
su
e di
su
.
Esempio
Consideriamo due distribuzioni aventi le seguenti modalità:
Possiamo determinare per tali distribuzioni i rispettivi scarti quadratici medi, e il valore della covarianza; effettuando i calcoli, si ottiene:
Poiché il coefficiente di correlazione è dato dal rapporto tra la covarianza e il prodotto delle deviazioni, abbiamo che:
Notiamo che il valore di
è molto prossimo a 1, il che indica che vi è una buona correlazione positiva.
Distribuzione normale
Una distribuzione normale è una distribuzione di frequenze caratteristica, in quanto essa può essere descritta da un grafico "a campana" simmetrico rispetto all'asse verticale che passa per il vertice (che corrisponde alla moda).
La distribuzione normale è una distribuzione teorica, e può descrivere un numero infinito di osservazioni.
Possiamo notare, inoltre, che l'area compresa tra la curva e l'asse delle ascisse racchiude la totalità delle osservazioni; e che la frequenza dei valori compresi tra due valori dell'ascissa
e
corrisponde all'area racchiusa dalla curva e dall'intervallo
.
Poiché la curva è simmetrica rispetto al suo asse verticale, si ha che la media e la mediana coincidono con la moda.
Tra le proprietà che caratterizzano queste distribuzioni, vi è il fatto che tra la media e una deviazione standard sono compresi circa il 34% dei valori della distribuzione; è quindi possibile, in ogni caso, determinare la percentuale dei valori che si trovano tra un generico valore
e la media.
Esempio
Consideriamo una distribuzione che abbia una media di 25, e uno scarto quadratico medio uguale a 3. Possiamo allora determinare la percentuale dei valori che si trovano tra 25 - 3 e 25 + 3, cioè i valori compresi tre 22 e 28.
Sapendo che tra la media e una deviazione standard cono compresi il 34% dei valori, possiamo concludere che tra 22 e 28 sono compresi (34 * 2)% = 68% dei valori.
Indici di forma
Nelle distribuzioni reali, quasi sempre ci si allontana dalla distribuzione standard, e questo si può notare anche dalla differente forma che assumono le distribuzioni.
In particolare, le distribuzioni possono presentare un'asimmetria, e in questo caso la media aritmetica si sposta, rispetto alla mediana, verso la parte di grafico che si schiaccia maggiormente.
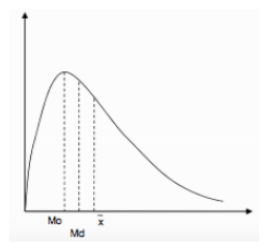
Oppure possono risultare più o meno appiattite, e in questo caso si parla di curtosi.
Accedi a tutti gli appunti
Tutor AI: studia meglio e in meno tempo
