Il reverendo Thomas Bayes e le probabiltà condizionate

Il matematico e teologo inglese Thomas Bayes (1702-1761) introdusse l'uso induttivo della probabilità e gettò le basi dell'inferenza statistica nel saggio: Sulla soluzione di un problema relativo alla dottrina del caso, che fu pubblicato pubblicato postumo nel 1763.

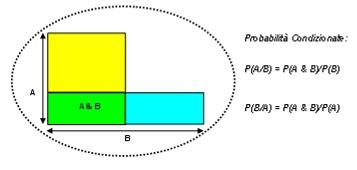
In figura le probabilità condizionate ed il teorema di Bayes sono illustrate con l'aiuto dei diagrammi di Eulero - Venn.
Supponiamo che l'intera area tratteggiata rappresenti l'unità in modo tale che l'area del rettangolo giallo-verde rappresenti la probabilità P(A) dell'evento A e quella del rettangolo azzurro-verde la probabilità P(B) dell'evento B. L'evento congiunto in cui sono veri sia A che B è rappresentato dal rettangolo verde avente probabilità P(A&B).
La probabilità condizionata che, essendosi verificato B si verifichi anche A, é data dalla definizione P(A/B) = P(A&B)/P(B) cioè rettangolo verde rapportato al rettangolo azzurro-verde.
Nel caso semplice di due soli eventi (A e B) il teorema di Bayes, che qualcuno chiama formula di Bayes, si ottiene facilmente eguagliando il termine P(A&B) ricavato dalle due definizioni di probabilità condizionata.
Il teorema ci dice come deve essere modificata la stima della probabilità P(A) dell'evento A alla luce della nuova informazione che l'evento B si è verificato.
Il metodo induttivo di soluzione dei problemi si può avvalere del teorema di Bayes nel senso che esso può indicare man mano, come aumenta la probabilità di veridicità di una ipotesi scientifica con il verificarsi di sperimentazioni che la confermino (vedi Gilles, Giorello, la filosofia della scienza nel XX secolo, Laterza 1995, pag. 19-22).
Tutte le organizzazioni possono avvalersi del modello bayesiano per valutare come, nel tempo e all'accrescersi delle informazioni disponibili, possa variare la probabilità dei rischi e delle opportunità, cui singoli progetti o intere aree di businness sono soggette (vedi R.Chiappi, il foglio elettronico come strumento di problem solving, F.Angeli 2009, pag. 180-182).
Problema di Monty Hall: in un gioco a quiz il conduttore invita il concorrente a scegliere tra tre porte, sapendo che dietro due ci sarà una capra (inutilizzabile) e dietro una un auto che potrà essere, se individuata, un ricco premio. Dunque la probabilità di vincità è di 1/3. Il concorrente sceglie una porta. Supponiamo ora che il conduttore apra una delle due porte rimaste chiuse per fornire una ulteriore informazione al giocatore (naturalmente aprirà comunque una porta dietro cui si trova una capra) prospettando al concorrente la facoltà di cambiare la porta da lui inizialmente scelta con l'unica rimasta chiusa. La maggior parte delle persone, tra cui il celebre matematico ungherese Paul Erdos, hanno sostenuto che cambiare o meno porta sia indifferente: prima le porte chiuse erano tre con probabilità di successo di 1/3 ora le porte chiuse sono due con probabilità di successo di 1/2. E' corretta questa posizione? Non è corretta perchè il conduttore, tra le due porte non scelte, aprirà obbligatoriamente quella che ha dietro una capra concentrando una probabilità di 2/3 sull'altra porta rimasta chiusa a fronte della probabilità di solo 1/3 di quella inizialmente scelta dal concorrente. Il teorema di Bayes indica correttamente:
P(A/B) = P(A) * P(B/A)/P(B) = 1/3 * [1/(1/2)] = 2/3.
Molti fisici e alcuni ingegneri sono convinti che le probabilità siano sempre e solo qualcosa di insito nel sistema che si sta studiando, invece in molte situazioni la stima delle probabilità dipende dal tipo e dalla quantità delle informazioni disponibili. Le aziende petrolifere, ad esempio, spendono soldi per effettuare test sismici sui giacimenti potenziali proprio allo scopo di accrescere le informazioni, ridurre le probabilità d'insuccesso ed affrontare i grandi investimenti di ricerca e sviluppo solo dove i risultati attesi sono allettanti ed i rischi sostenibili.