Concavità di una funzione
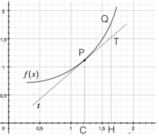
• Una funzione presenta concavità verso l’alto in un intorno completo di x0, se in tale intorno f(x)>tg(x0);
• Una funzione presenta concavità verso il basso in un intorno completo di x0, se in tale intorno f(x)
I punti in cui cambia la concavità sono definiti punti di flesso. Il flesso può a sua volta essere ascendente se si passa da concavità verso il basso a concavità verso l’altro e discendente se si passa da concavità verso l’alto a concavità verso il basso.
Altri teoremi delle funzioni derivabili
Teorema di Cauchy: Se f(x) e g(x) sono continue e definite in [a,b], derivabili in ]a,b[ e g’(x)≠0 in ]a,b[⇒∃x0∊[a,b]|(f'(x_0))/(g'(x_0))=(f(b)-f(a))/(g(b)-g(a)).
Teorema di De L’Hopital: Il primo caso si utilizza per risolvere FI[0/0] ed è applicabile se: f(x) e g(x) sono continue in [a,b] (può essere continua anche solamente a destra o sinistra), derivabili in ]a,b[, danno vita a una FI[0/0] per x→x0, g’(x0)≠0 e lim┬(x→x_0 ) ((f'(x))/(g'(x)))=l⇒lim┬(x→x_0 ) ((f(x))/(g(x)))=l.
Di fatto è sufficiente controllare che valgano le prime tre condizioni, perchè le altre si verificano applicando il teorema.
Se dopo aver applicato il teorema si ottiene un’altra FI[0/0] lo si riapplica.
Il teorema è poi estendibile alle FI ∞/∞, 0⋅∞(riconducibile a ∞/∞o 0/0),0^0 ∞^0 1^∞(f〖(x)〗^(g(x))=e^(g(x)ln(f(x))), lo si applica all’esponente).







 Accedi a tutti gli appunti
Accedi a tutti gli appunti
 Tutor AI: studia meglio e in meno tempo
Tutor AI: studia meglio e in meno tempo