Alla fine degli anni 70, una organizzazione commerciale ha individuato la possibilità di collocare vantaggiosamente su mercati esteri cinque diversi prodotti (Pi) nei quantitativi indicati sotto:
P1 = 100,000
P2 = 50,000
P3 = 120,000
P4 = 300,000
P5 = 180,000
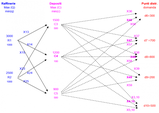
L’organizzazione selezionò alcune aziende artigiane (A1, A2, A3, A4, A5, A6) in grado di fornire in tempo utile i prodotti richiesti. I tecnici sapevano però bene che le aziende in questione avevano capacità produttive limitate. Inoltre il management e l’ufficio acquisti ritenevano fosse piuttosto rischioso, anche se il livello di qualità offerto è valutato simile per tutte le sei aziende, concentrare le forniture solo sulle aziende che offrivano costi più contenuti, a causa del timore che non potessero essere rispettati i tempi di consegna.
La direzione diede comunque disposizioni all’ufficio Ricerca Operativa dell’azienda affinché analizzasse il problema e fornisse indicazioni utili per supportare le decisioni del management.
Indice
Soluzione illimitata
L’ufficio ricerca operativa disponeva di un terminale 3780 della IBM da cui poteva accedere al package MPS-X disponibile in libreria. Il sistema in questione poteva risolvere la quasi totalità dei problemi di PL, a variabili continue, intere o miste che si possono presentare nella realtà economica o aziendale. Il package consentiva di trattare problemi di PL continua sino a molte migliaia di vincoli e più di un milione di variabili. Più ristretta la dimensione dei modelli se il problema era a numeri interi o misti. In questo caso infatti il sistema deve alternare il metodo del Simplesso con il Branch and Bound.Per prima cosa l’ufficio intendeva ricercare l’allocazione a costo minimo delle commesse indipendentemente da qualunque vincolo sulla capacità produttiva delle aziende artigiane o sui rischi di ritardo Una assunzione teorica che consentiva rapidamente di ottenere un limite inferiore dei Costi che dovevano essere sostenuti. Per fare questo è necessario prendere in considerazione la matrice dei costi di produzione Cij, riportata sotto per ogni prodotto Pi e ogni azienda Aj.
Gli unici vincoli di cui si tiene conto in questa analisi iniziale, oltre alle quantità richieste per ciascun prodotto, sono quelli della indisponibilità di alcune aziende a fornire alcuni prodotti. Specificatamente:
A1 non produce P4
A4 non produce P5
A6 non produce P2
A6 non produce P4
Tuttavia, per non appesantire il modello con altri 4 vincoli, i tecnici di R.O. decidono di usare il metodo delle penalità. In pratica si tratta di introdurre dei Costi molto alti (nell’esempio Cij = 9999) nelle celle che si vogliono scartare. In questa maniera, poiché si tratta di un problema di minimo, il metodo del simplesso scarterà automaticamente allocazioni maggiori di zero in queste celle.
| Prodotti i | P1 | P2 | P3 | P4 | P5 |
| Aziende j | |||||
| A1 | 950 | 1850 | 1000 | 9999 | 980 |
| A2 | 880 | 1730 | 900 | 750 | 920 |
| A3 | 1000 | 1950 | 960 | 720 | 950 |
| A4 | 980 | 1800 | 950 | 700 | 9999 |
| A5 | 1020 | 2000 | 980 | 810 | 930 |
| A6 | 1100 | 9999 | 1000 | 9999 | 1000 |
Xij = quantità di prodotti i acquistati dall’azienda j
Z = funzione oggetto (o obiettivo) da minimizzare
Il modello di PL continua sarà:
( Z = mbox{min} (sumsum Xij ast Cij ) mbox{ con:} (i = 1,ldots 5) mbox{ e } (j = 1, …6))
Con i vincoli:
(P1 = sum X1j = 100,000, (j = 1,…6) )
( P2 = sum X2j = 50,000, (j = 1,…6) )
( P3 = sum X3j = 120,000, (j = 1,…6) )
( P4 = sum X4j = 300,000, (j = 1,…6) )
( P5 = sum X5j = 180,000, (j = 1,…6) )
Ecco sotto il risultato ottenuto, con l’evidenza del Costo Minimo:
| Prodotti i | P1 | P2 | P3 | P4 | P5 | Totali | |
| Aziende j | |||||||
| A1 | 0 | 0 | 0 | 0 | 0 | 0 | |
| A2 | 100,000 | 50,000 | 120,000 | 0 | 180,000 | 450,000 | |
| A3 | 0 | 0 | 0 | 0 | 0 | 0 | |
| A4 | 0 | 0 | 0 | 300,000 | 0 | 300,000 | |
| A5 | 0 | 0 | 0 | 0 | 0 | 0 | |
| A6 | 0 | 0 | 0 | 0 | 0 | 0 | Costo Min |
| Totali | 100,000 | 50,000 | 120,000 | 300,000 | 180,000 | 750,000 | 658,100,000 |
| Tot. richiesti | 100,000 | 50,000 | 120,000 | 300,000 | 180,000 |
Soluzione limitata
Stabilito che la spesa sarà comunque superiore a 658.1 milioni di Lit (i tecnici di R.O. sanno bene che l’aggiunta di vincoli ad un problema non potrà che peggiorare il valore ottimo della funzione obiettivo) viene eseguito un Run introducendo nel modello i vincoli dij che, le j aziende artigiane hanno sulla massima produzione possibile per ciascun prodotto iNel seguito è riportata la tabella delle produzioni massime dij per ciascuna azienda e ciascun prodotto:
| Prodotti i | P1 | P2 | P3 | P4 | P5 |
| Aziende j | |||||
| A1 | 40,000 | 20,000 | 60,000 | 0 | 50,000 |
| A2 | 30,000 | 30,000 | 50,000 | 100,000 | 60,000 |
| A3 | 40,000 | 30,000 | 60,000 | 150,000 | 60,000 |
| A4 | 60,000 | 40,000 | 100,000 | 200,000 | 0 |
| A5 | 50,000 | 30,000 | 80,000 | 150,000 | 80,000 |
| A6 | 20,000 | 0 | 40,000 | 0 | 50,000 |
( Z = mbox{min } (sum sum Xij ast Cij ) mbox{ con: } (i = 1,…5) e (j = 1, …6) )
Con i vincoli:
(P1 = sum X1j = 100,000, (j = 1,ldots 6) )
( P2 = sum X2j = 50,000, (j = 1,ldots 6) )
( P3 = sum X3j = 120,000, (j = 1ldots 6) )
( P4 = sum X4j = 300,000, (j = 1, ldots 6) )
( P5 = sum X5j = 180,000, (j = 1, ldots 6) )
( Xij le dij mbox{ con: } (i = 1, ldots 5) e (j = 1, ldots6) )
Ecco il risultato ottenuto. Come previsto il Costo Minimo è sensibilmente aumentato:
| Prodotti |
P1 | P2 | P3 | P4 | P5 | Totali | |
| Aziende |
|||||||
| A1 | 40,000 | 0 | 0 | 0 | 0 | 40,000 | |
| A2 | 30,000 | 30,000 | 50,000 | 0 | 60,000 | 170,000 | |
| A3 | 0 | 0 | 0 | 100,000 | 40,000 | 140,000 | |
| A4 | 30,000 | 20,000 | 70,000 | 200,000 | 0 | 320,000 | |
| A5 | 0 | 0 | 0 | 0 | 80,000 | 80,000 | |
| A6 | 0 | 0 | 0 | 0 | 0 | 0 | Costo Min |
| Totali | 100,000 | 50,000 | 120,000 | 300,000 | 180,000 | 750,000 | 672,800,000 |
| Tot. richiesti | 100,000 | 50,000 | 120,000 | 300,000 | 180,000 |
Non più di 3 commesse per azienda (soluzione greedy)
Introducendo infine il vincolo, voluto dalla direzione, per evitare ritardi nella consegna dei prodotti, si rispetta la decisione di non affidare più di 3 commesse a ciascuna azienda artigiana. Il Team di ricerca operativa sa bene che l’introduzione di questo ulteriore vincolo implica un salto di qualità nella modellistica in quanto non si può più utilizzare la programmazione lineare continua e quindi l’efficiente metodo del Simplesso. Per avere rapidamente un risultato (approssimato per eccesso) sui costi da sostenere introducendo i 6 nuovi vincoli (uno per ciascuna azienda j) si decide di cercare una soluzione mediante la euristica greedy della “matrice minima”.Questo metodo consiste nell’esaminare la matrice dei costi ed iniziare assegnando il massimo possibile, in base alle disponibilità dij, alla cella (cioè alla accoppiata azienda prodotto) che presenta il costo minimo. Si procede poi a selezionare, tra le celle rimanenti, quelle a costo più basso e così via. In questo processo oltre a controllare di non superare mai nelle assegnazioni il valore dij si deve controllare di non superare le 5 richieste Pi di ciascun prodotto e il numero di assegnazioni alle aziende (non più di 3). Quando la richiesta di un prodotto è saturata si cancella l’intera colonna. Quando una azienda ha ricevuto 3 assegnazioni si cancella l’intera riga. Sotto è riportato il risultato del processo:
| Prodotti | P1 | P2 | P3 | P4 | P5 |
| Aziende | |||||
| A1 | 950 | 1850 | 9999 | 980 | |
| A2 | 880 | 900 | 920 | ||
| A3 | 1950 | 720 | 950 | ||
| A4 | 980 | 950 | 700 | 9999 | |
| A5 | 930 | ||||
| A6 | 9999 | 9999 |
| Prodotti | P1 | P2 | P3 | P4 | P5 |
| Aziende | |||||
| A1 | 40,000 | 20,000 | 60,000 | 0 | 50,000 |
| A2 | 30,000 | 30,000 | 50,000 | 100,000 | 60,000 |
| A3 | 40,000 | 30,000 | 60,000 | 150,000 | 60,000 |
| A4 | 60,000 | 40,000 | 100,000 | 200,000 | 0 |
| A5 | 50,000 | 30,000 | 80,000 | 150,000 | 80,000 |
| A6 | 20,000 | 0 | 40,000 | 0 | 50,000 |
| Prodotti |
P1 | P2 | P3 | P4 | P5 | Totali | Commesse | |
| Aziende | X Azienda | |||||||
| A1 | 40,000 | 20,000 | 60,000 | 2 | ||||
| A2 | 30,000 | 50,000 | 60,000 | 140,000 | 3 | |||
| A3 | 30,000 | 100,000 | 40,000 | 170,000 | 3 | |||
| A4 | 30,000 | 70,000 | 200,000 | 300,000 | 3 | |||
| A5 | 80,000 | 80,000 | 1 | |||||
| A6 | 0 | Costo Min | 0 | |||||
| Totali | 100,000 | 50,000 | 120,000 | 300,000 | 180,000 | 750,000 | 680,400,000 | |
| Tot. richiesti | 100,000 | 50,000 | 120,000 | 300,000 | 180,000 |
Per chi volesse approfondire gli algoritmi greedy e la loro traduzione in un codice (nello specifico Visual Basic) si rimanda al riferimento citato: “Problemi, Algoritmi e Codici, di Smith e Hume”.
Non più di 3 commesse per azienda (soluzione del simplesso più branch and bound)
Per formulare il problema come programmazione lineare a numeri misti (variabili continue e intere) è necessario introdurre oltre le 30 (5 Prodotti per 6 Aziende) variabili continue Xij altre 30 variabili bivalenti Yij. In definitiva riassumendo l’intero modello:
Pi numero di pezzi da produrre per ciascun prodotto i
Aj aziende artigiane individuate dalla organizzazione commerciale
Cij costo di una unita del prodotto i se fornito dall’azienda j
dij produzione massima possibile del prodotto i da parte della azienda j
Xij quantità di prodotto i acquistato dall’azienda j
Yij variabile intera bivalente. Yij = 1 se si acquista i da j. Yij = 0 in caso contrario.
Z funzione oggetto da minimizzare
( Z = mbox{ min } ( sum sum Xij ast Cij ) mbox{ con: } (i = 1,…5) mbox{ e } (j = 1, …6) )
Con i vincoli:
Sulla richiesta di prodotti
( P1 = sum X1j = 100,000 (j = 1, ldots 6) )
( P2 = sum X2j = 50,000 (j = 1, ldots 6) )
( P3 = sum X3j = 120,000 (j = 1, ldots 6) )
( P4 = sum X4j = 300,000 (j = 1, ldots 6) )
( P5 = sum X5j = 180,000 (j = 1, ldots 6) )
Sulla capacità delle aziende
( Xij le dij ast Yij mbox{ con: } (i = 1, ldots 5) mbox{ e } (j = 1, ldots 6) )
Sui rischi (non più di tre commesse per azienda)
( A1 = sum Yi1 le 3 (i = 1, ldots 5) )
( A2 = sum Yi2 le 3 (1 = 1, ldots 5) )
( A3 = sum Yi3 le 3 (1 = 1, ldots 5) )
( A4 = sum Yi4 le 3 (1 = 1, ldots 5) )
( A5 = sum Yi5 le 3 (1 = 1, ldots 5) )
( A6 = sum Yi6 le 3 (1 = 1, ldots 5) )
Variabili continue positive ( Xij ge 0 mbox{ con: } (i = 1, ldots 5) mbox{ e } (j = 1, ldots 6) )
Variabili intere bivalenti ( Yij = 0 mbox{ o } 1 mbox{ con: } (i = 1, ldots 5) mbox{ e } (j = 1, ldots 6) )
Di seguito sono riportati i risultati ottenuti con il modello sopra descritto che rispecchia la formulazione completa del problema (include anche i vincoli di non più di tre commesse per azienda):
| Prodotti | P1 | P2 | P3 | P4 | P5 |
| Aziende | |||||
| A1 | 950 | 1850 | 1000 | 9999 | 980 |
| A2 | 880 | 1730 | 900 | 750 | 920 |
| A3 | 1000 | 1950 | 960 | 720 | 950 |
| A4 | 980 | 1800 | 950 | 700 | 9999 |
| A5 | 1020 | 2000 | 980 | 810 | 930 |
| A6 | 1100 | 9999 | 1000 | 9999 | 1000 |
| Prodotti | P1 | P2 | P3 | P4 | P5 |
| Aziende | |||||
| A1 | 40,000 | 20,000 | 60,000 | 0 | 50,000 |
| A2 | 30,000 | 30,000 | 50,000 | 100,000 | 60,000 |
| A3 | 40,000 | 30,000 | 60,000 | 150,000 | 60,000 |
| A4 | 60,000 | 40,000 | 100,000 | 200,000 | 0 |
| A5 | 50,000 | 30,000 | 80,000 | 150,000 | 80,000 |
| A6 | 20,000 | 0 | 40,000 | 0 | 50,000 |
| Prodotti | P1 | P2 | P3 | P4 | P5 | Totali | Massimo |
| Aziende | |||||||
| A1 | 1 | 1 | 0 | 0 | 0 | 2 | 3 |
| A2 | 1 | 0 | 1 | 0 | 1 | 3 | 3 |
| A3 | 1 | 0 | 0 | 1 | 1 | 3 | 3 |
| A4 | 0 | 1 | 1 | 1 | 0 | 3 | 3 |
| A5 | 0 | 0 | 0 | 0 | 1 | 1 | 3 |
| A6 | 0 | 0 | 0 | 0 | 0 | 0 | 3 |
| Prodotti | P1 | P2 | P3 | P4 | P5 |
| Aziende | |||||
| A1 | 40,000 | 20,000 | 0 | 0 | 0 |
| A2 | 30,000 | 10,000 | 50,000 | 0 | 60,000 |
| A3 | 40,000 | 0 | 0 | 150,000 | 60,000 |
| A4 | 0 | 40,000 | 100,000 | 200,000 | 0 |
| A5 | 0 | 0 | 0 | 0 | 80,000 |
| A6 | 0 | 0 | 0 | 0 | 0 |
| Prodotti | P1 | P2 | P3 | P4 | P5 | Totali | |
| Aziende | |||||||
| A1 | 40,000 | 10,000 | 0 | 0 | 0 | 50,000 | |
| A2 | 30,000 | 0 | 50,000 | 0 | 60,000 | 140,000 | |
| A3 | 30,000 | 0 | 0 | 100,000 | 40,000 | 170,000 | |
| A4 | 0 | 40,000 | 70,000 | 200,000 | 0 | 310,000 | |
| A5 | 0 | 0 | 0 | 0 | 80,000 | 80,000 | |
| A6 | 0 | 0 | 0 | 0 | 0 | 0 | Costo Min |
| Totali | 100,000 | 50,000 | 120,000 | 300,000 | 180,000 | 750,000 | 676,000,000 |
| Tot. richiesti | 100,000 | 50,000 | 120,000 | 300,000 | 180,000 |
“La soluzione fornita dall’elaboratore comporta un costo di (680,400,000 – 676,000,000) = 4,400,000 Lit. meno della soluzione euristica precedentemente trovata.
Può essere, a questo punto utile qualche considerazione. Un Run di questo tipo impiegando 15.02 secondi di CPU, 27.30 secondi di Iinput/Output, e occupando circa 260 Kbytes di memoria ha un costo di circa 10.000 Lit. (10.000 Lit dell’epoca valgono circa 34 Eur di oggi), ben poca cosa quindi se raffrontata al risparmio ottenuto; d’altro canto si deve anche ricordare che vi sono altri costi per la messa a punto del modello di PLNM e della sua implementazione in macchina, ma soprattutto si deve osservare che molto spesso aziende medio piccole non dispongono di un terminale capace di contenere packages di queste dimensioni”.
Ricorrendo al Risolutore ed al file Excel indicato si invitano i lettori interessati a ripercorrere tutti i risultati ottenuti con MPSX inoltre, con riferimento all’ultimo Run, che utilizza variabili continue Xij e variabili bivalenti Yij, si propone di esplorare tre nuove situazioni:
- Non più di 2 commesse per azienda,
- Quantitativi di P2 e P3 doppi,
- Non più di 2 commesse per azienda e quantitativi di P2 e P3 doppi.
Conclusioni
Naturalmente oggi le potenzialità dei computer sono molto diverse da quelle di quasi 50 anni fa. Ma i metodi di risoluzione dei problemi sono poco diversi. L’algoritmo del Simplesso di Dantzig, per i problemi di programmazione lineare, cosi come quello di Land e Doig (Branch and Bound) per i problemi a numeri interi sono sempre validi, anche se progressi nei metodi e algoritmi sono stati fatti (e riportati da Frontline anche in Excel) con nuovi approcci , come ad esempio gli algoritmi genetici e i vincoli alldifferent : vedi il riferimento citato: “Programmazione matematica, di Hume e Smith”.Il Branch and Bound prevede che ad ogni nodo dell’albero rovesciato, costruito per esplorare le varie soluzioni intere, si risolva un Simplesso, dunque nella tabella riassuntiva riportata sotto il numero dei nodi equivale al numero di volte in cui si è applicato il Simplesso per risolvere il problema. Sostanzialmente, anche se non è esattamente così, ad ogni nodo ci si assicura che una variabile intera lo sia effettivamente. Naturalmente ad ogni Run non si riparte dall’inizio ma ci si avvale dei risultati ottenuti in precedenza.
| Problema: | Costi minimi ( [math]10^6[/math] Lit) |
N° nodi |
|---|---|---|
| Soluzione illimitata | 658.1 | 1 |
| Soluzione limitata | 672.8 | 1 |
| Max 3 Commesse per azienda | 676.0 | 16 |
| ” Soluzione Greedy | 680.4 | -- |
| ” P2 e P3 doppi | 886.1 | 24 |
| Max 2 Commesse per azienda | 682.3 | 34 |
| ” P2 e P3 doppi | impossibile | -- |
Una seconda considerazione è che le soluzioni euristiche, come quelle di tipo Greedy, danno in generale buoni risultati (680.4), ma sempre peggiori (o nei casi fortunati uguali) a quelli ottenuti applicando la Programmazione matematica (676).
Si può poi osservare che anche senza aggiungere vincoli, ma rendendo quelli esistenti più restrittivi
la soluzione trovata peggiora: con un massimo 3 commesse per azienda (676), con un massimo di 2 commesse per azienda 682.3. Se poi raddoppiamo i quantitativi richiesti per P2 e P3 si passa addirittura da un costo di 676 ad un costo di 886.1.
Infine se pretendiamo contemporaneamente di raddoppiare i valori di P2 e P3 e non assegnare più di due commesse a ciascuna azienda il problema diviene impossibile, cioè la regione delle soluzioni ammissibili si è ristretta tanto sino a diventare vuota.
Riferimenti
- Il foglio elettronico come strumento per il Problem Solving, R. Chiappi, Franco Angeli, Milano 2008.
- Project Management, Problem Solving, Decision Making, R Chiappi, Matematicamente.it 2015
- Programmazione matematica, di Hume e Smith
- Programmazione lineare, di Roberto Chiappi
- Problemi, Algoritmi e Codici, di Smith e Hume
- Piani di produzione, di Roberto Chiappi
- Allocazione degli investimenti di Roberto Chiappi
- Raffineria, di Roberto Chiappi
- Goal Programming: scelta dei titoli su cui investire, di Roberto Chiappi

![La programmazione lineare [George B. Dantzig]](https://cdn.skuola.net/shared/thumb/159x141/news_foto/images/stories/problem_solving/dantzig.png)





 Accedi a tutti gli appunti
Accedi a tutti gli appunti
 Tutor AI: studia meglio e in meno tempo
Tutor AI: studia meglio e in meno tempo