[math](4-2x)(x+3)+(3x-13)(1-x)>=-x(2x+1)-(x-12)[/math]
[math](4-2x)(x+3)+(3x-13)(1-x)>=-x(2x+1)-(x-12)[/math]
;
[math]4x+12-2x^2-6x+3x-3x^2-13+13x>=-2x^2-x-x+12[/math]
;
Semplificando
[math](-2-3+2)x^2+(4-6+3+13+1+1)x+12-13-12>=0[/math]
;
[math]-3x^2+16x-13>=0[/math]
Cambiando di segno si ha:
[math]3x^2-16x+13>=0[/math]
Risolviamo la disequazione di secondo grado
[math]3x^2-16x+13>=0[/math]
[math]Delta=b^2-4ac=(-16)^2-(4 \cdot (13) \cdot 3)=256-156=100[/math]
[math]x_(1,2)=(-b+-\sqrt{Delta})/(2a)=(16+-\sqrt(100))/6=(16+-(10))/6 => x_1=1 ^^ x_2=(13)/3[/math]
.
Siccome il coefficiente di
[math]x^2[/math]
e il segno della disequazione sono discordi,prenderemo come soluzione accettabile l'intervallo interno,
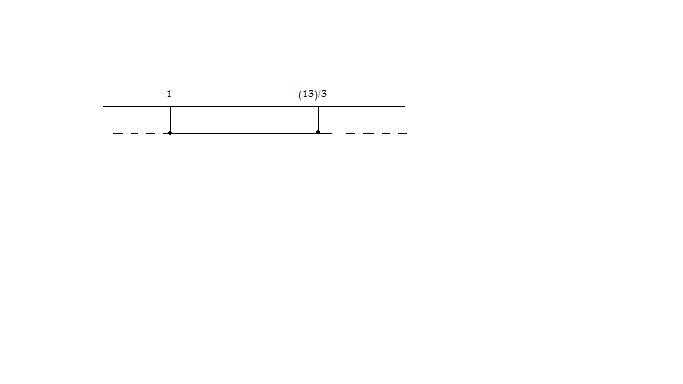
per cui la soluzione sarà:
[math]1>=x>=(13)/3[/math]
.
Accedi a tutti gli appunti
Tutor AI: studia meglio e in meno tempo
