[math]2(x+3)(x-3)+18>2x^2-((x-1)(4x+8))/2[/math]
[math]2(x+3)(x-3)+18>2x^2-((x-1)(4x+8))/2[/math]
;
[math]2(x^2-9)+18>2x^2-(4x^2+8x-4x-8)/2[/math]
;
[math]2x^2-18+18>2x^2-(4x^2+4x-8)/2[/math]
;
Semplificando
[math]-(4(x^2+x-2))/2>0[/math]
Continuando a semplificare e cambiando di segno si ha:
[math]2(x^2+x-2)>0[/math]
;
Dividendo ambo i membri per
[math]2[/math]
, otteniamo
[math]x^2+x-2>0[/math]
Risolviamo l'equazione di secondo grado
[math]Delta=b^2-4ac=(1)^2-(4 \cdot (-2) \cdot 1)=1+8=9[/math]
[math]x_(1,2)=(-b+-\sqrt{Delta})/(2a)=(-1+-\sqrt9)/2=(-1+-(3))/2 => x_1=-2 ^^ x_2=1[/math]
.
Siccome il coefficiente di
[math]x^2[/math]
e il segno della disequazione sono concordi,prenderemo come soluzione accettabile l'intervallo esterno.
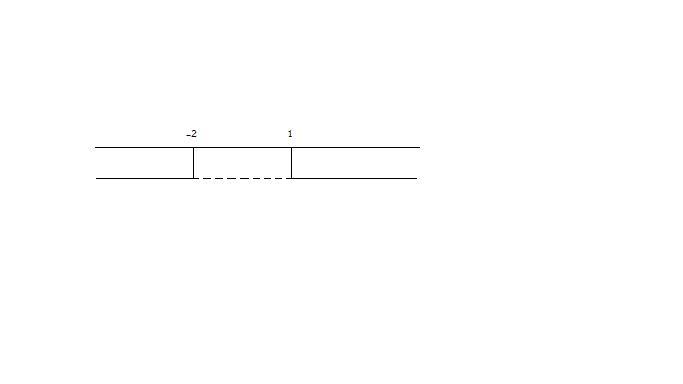
per cui la soluzione sarà:
[math]x>-2 vv x>1[/math]
.
Accedi a tutti gli appunti
Tutor AI: studia meglio e in meno tempo
