In un triangolo rettangolo l'area è
[math]21450 dm^2[/math]
e i cateti sono uno i
[math]3/4[/math]
dell'altro.
Calcola il perimetro del triangolo.
Indice
Soluzione
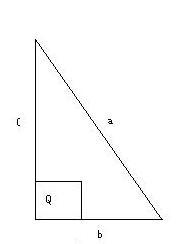
Dati
[math]b=3/4c[/math]
[math]A=21450 dm^2[/math]
Svolgimento
Dividendo
[math]c[/math]
in
[math]4[/math]
segmenti uguali,
[math]b[/math]
è lungo
[math]3[/math]
parti.
Il rettangolo di lati
[math]b[/math]
e
[math]c[/math]
è formato da
[math]4 \cdot 3=12[/math]
quadratini Q uguali.
La superficie del triangolo, essendo la metà, è formata da
[math]6[/math]
quadratini
[math]Q[/math]
.
Perciò l'area vale:
[math]Q=(21450 dm^2)/6=3575dm^2[/math]
Quindi ogni lato del quadratino è dato dalla formula
[math]u=\sqrt{Q}=\sqrt(3575 dm^2)=59,79dm[/math]
che rappresenta la misura di una singola parte, e perciò si ha:
[math]c=4u=4 \cdot 59,79 dm=239,16 dm[/math]
[math]b=3u=3 \cdot 59,79 dm=179,37 dm[/math]
Per il Teorema di Pitagora
[math]a=\sqrt{(b)^2+(c)^2}=\sqrt((179,37 dm)^2+(239,16 dm)^2)=\sqrt(32173,60+57197,50) dm=[/math]
[math]=\sqrt{89371,10} dm=298,94 dm[/math]
Pertanto
[math]2p=a+b+c=(298,94+179,37+239,16) dm=717,47 dm[/math]
.
Accedi a tutti gli appunti
Tutor AI: studia meglio e in meno tempo
