Esplorazione delle curve matematiche: un viaggio tra storia e geometria

Luciano Cresci, Le curve celebri.

Invito alla storia della matematica attraverso le curve piane più affascinanti,

Franco Muzzio Editore, Padova, 1998, pp. 200, lire 24.000 .

Descrizione delle equazioni matematiche

L'autore si propone di percorrere la storia del pensiero matematico attraverso brevi descrizioni delle curve piane, che per vari motivi sono divenute famose.

Per ciascuna curva è riportata la notazione matematica che permette di rappresentarla: a volte l'equazione cartesiana, altre le equazioni parametriche, altre ancora l'equazione polare.

L' equazione cartesiana è quella che lega l' ascissa x con l' ordinata y riferite ad un sistema di assi cartesiani . Per esempio, x² +y² =1 rappresenta un cerchio, x² -y² =1 un'iperbole, x² +2y² =1 un'ellisse, y=x² una parabola.

Equazioni parametriche e curve notevoli

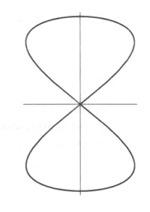
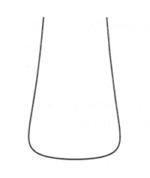
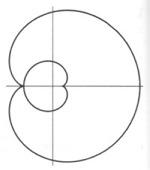
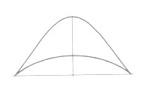
Le equazioni parametriche sono invece due per ciascuna curva del piano; hanno questo nome perché l'ascissa x e la ordinata y si ottengono per mezzo di un parametro variabile t. Per esempio, la lemniscata , una curva a forma di otto, ha equazioni x=sint•cost, y=cost; la pera ha equazioni x=1+cost, y=1/(1+sint); la cardioide ha equazioni x=2cost-cos2t, y=2sint-sin2t. Il bicorno , o cappello a due punte, ha equazioni x=cost, y=sin² t/(2+sint).

Equazioni polari e cicloide

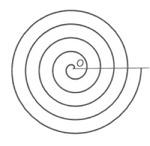
L' equazione polare di una curva è una relazione che lega la distanza r, di un generico punto P (della curva) dall'origine O ( polo ), con l'angolo ß, formato dalla retta OP con una semiretta fissata (asse polare ). Solitamente si usano le lettere greche RO e TETA; per esigenze di caratteri ho usato r e ß. Un esempio è costituito dalla spirale di Archimede: r=ß.

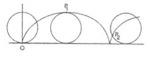
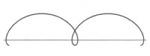
Tra le curve di particolare interesse non poteva mancare un'analisi storica della cicloide o roulette. La curva, studiata per primo da Pascal, è il percorso che fa nell'aria il punto di una ruota, quando questa compie una rotazione completa. Le sue equazioni parametriche sono x=r(t-sint), y=r(1-cost). Può essere estesa se il punto è posto all'esterno della circonferenza, contratta se il punto è all'esterno delle circonferenza. Da ricordare il paradosso della cicloide estesa. Le ruote del treno, per esempio, hanno una flangia che fuoriesce dalla ruota vera e propria e serve per non far uscire la ruota dal binario. Mentre la ruota rotola sul binario un punto della flangia esterna descrive una cicloide con un piccolo cappio. Proprio mentre descrive questo cappio, il punto è costretto a tornare indietro. Da qui il paradosso: come è possibile che i punti della flangia tornino indietro mentre il treno avanza?

Catenaria e curve del secolo scorso

Un'altra curva particolarmente interessante è la catenaria , studiata da Huygens. E' la curva formata da una catena, o anche dal cavo della luce, sospesa ai suoi estremi. L'equazione cartesiana è y=(a/2)•cosh(x/a), ricordando la definizione di coseno iperbolico y= (a/2)(e^x/a +e^-x/a ).

Infine la famosa curva a campana di Gauss particolarmente importante nelle distribuzioni statistiche.

Nel libro non mancano i riferimenti alle curve del secolo scorso: la curva di Peano, la polvere di Cantor, la curva di Kock, i frattali di Mandelbrot.

Un libro che incuriosisce, unendo notizie storiche, equazioni e disegni piacevoli.

Antonio Bernardo

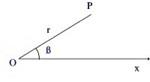
Il punto P in coordinate polari P(r,ß)

Lemniscata

Pera

Cardioide

Bicorno

Spirale di Archimede

Cicloide

La cicloide estesa presenta un paradosso: mentre la ruota avanza alcuni suoi punti tornano indietro in prossimità del cappio centrale.