D'Ignazio e Suppa, Il problema geometrico dal compasso al cabri

Il problema geometrico, dal compasso al Cabri

di

I. D'Ignazio e E. Suppa

La scuola geometrica di F. Enriques, uno dei più grandi geometri del secolo scorso, aveva dato una forte spinta innovativa all'insegnamento della matematica in Italia, in particolar modo all'insegnamento della geometria. L'approccio euclideo, di tipo logico-sintetico, era ritenuto nella massima considerazione. L'opera "Questioni riguardanti le Matematiche elementari", diretta da Enriques, alla quale avevano partecipato ricercatori di primo piano ma anche 'bravi' insegnanti delle scuole medie, aveva avvicinato la matematica degli studenti a quella della ricerca pura.

Il metodo sintetico era ritenuto altamente formativo.

Con il passare dei decenni, l'approccio analitico di tipo algebrico-numerico ha gradualmente preso il primo posto nella metodologia degli insegnanti. Probabilmente una delle spinte in questa direzione è stata data dallo sviluppo dell'informatica, la quale fa uso essenzialmente di numeri ed equazioni. I nuovi software con una interfaccia grafica sempre più avanzata hanno riportato in auge i problemi geometrici risolubili per via sintetica: i cosiddetti problemi risolubili con riga e compasso. Cabri-Géométre permette di disegnare le figure ma anche di manipolarle e deformarle con continuità: puntando con il mouse alcuni punti, si può vedere cosa cambia e cosa resta inalterato di una figura. In questo modo si possono formulare congetture che hanno un buon grado di probabilità di essere vere e si può intravedere la strada per dimostrare sinteticamente le proprietà richieste.

Il manuale di D'Ignazio e Suppa può apparire a prima vista anacronistico perché riprende i metodi classici per risolvere i problemi geometrici, invece esso, riallacciandosi alla tradizione dei geometri italiani, e sfruttando al massimo le caratteristiche didattiche di Cabri, si pone all'avanguardia nella didattica della matematica, forse anche troppo per essere apprezzato dagli insegnati di oggi. Tuttavia, è da osservare che il nuovo esame di stato per la maturità scientifica si sta liberando dagli esercizi standard di applicazione dell'analisi matematica per riproporre qualche questione di geometria sintetica. Può essere un segnale che la 'vecchia' geometria di Euclide non è affatto morta.

Due esempi per illustrare l'aiuto che può dare Cabri nella risoluzione di problemi per via sintetica.

1. Di un triangolo ABC variabile, rimane fisso il lato BC e costante la lunghezza della mediana CM=m. Si chiede il lungo descritto dal punto A.

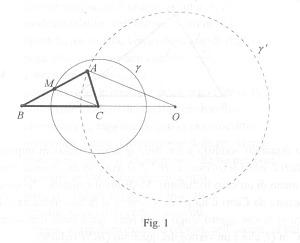
Per disegnare con Cabri il luogo descritto da A, fissiamo sullo schermo il segmento BC e tracciamo la circonferenza (gamma) di centro C e raggio m. Utilizzando il comando 'punto su un oggetto', collochiamo su di essa un punto M e chiediamo a Cabri di determinare il punto A simmetrico di B rispetto a M. Con il comando 'luogo di punti' facciamo tracciare il luogo di A mentre si fa percorrere ad M la circonferenza gamma. Si osserva che Cabri disegna una circonferenza che visivamente appare il doppio di quella precedente. Variando i parametri utilizzati, si osserva che queste osservazioni vengono confermate. A questo punto non resta che provare la congettura che Cabri suggerisce. Una dimostrazione potrebbe essere la seguente. Tracc iato un triangolo ABC e la sua mediana CM, mandiamo da A la parallela a CM che incontri la retta BC in O; i trinagoli ABO e MBC sono simili ed il rapporto di similitudine è 2. Pertanto, OB=2*BC e OA=2m. Ciò conferma che il luogo richiesto è una circonferenza di raggio 2m avente centro nel punto O simmetrico di B rispetto a C.

2. In un triangolo ABC inscrivere un quadrato avente due vertici su BC, un vertice su AB ed un vertice su AC.

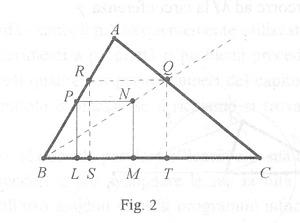
Tracciamo un triangolo ABC e con il comando "punto su un oggetto", prendiamo un punto P qualsiasi del lato AB. Mandiamo da P la perpendicolare PL al lato BC. Ora è facile disegnare il quadrato PLMN di lato PL. Questo quadrato soddisfa a tre delle quattro condizioni imposte dal problema; infatti L ed M si trovano su BC, P si trova su AB, mentre N non si trova su AB. Con il comando 'luogo di punti' si fa tracciare il luogo di N mentre P descrive il lato AB. Si vede che il luogo descritto da N è una retta che interseca il lato AC in un punto Q. Il quadrato richiesto è QRST.

Il testo, unico nel suo genere in italiano, è senz'altro utile agli insegnanti di matematica delle scuole secondarie, sia per ripassare i classici problemi della geometria sintetica sia per familiarizzare con Cabri

L'indice del libro

Capitolo I, Le costruzioni fondamentali

Capitolo II, Luoghi geometrici

Capitolo III, La ricerca dei luoghi geometrici

Capitolo IV, Le isometrie

Capitolo V Il metodo di traslazione

Capitolo VI, la rotazione e la simmetria centrale nella risoluzione dei problemi

Capitolo VII, La simmetria assiale nella risoluzione dei problemi

Capitolo VIII La similitudine

Capitolo IX, L'inversione circolare

Capitolo X, La geometria del triangolo

Per richiedere una copia fare riferimento a

FERRETTI
Via Pannella 56
64100 TERAMO

Tel.Fax 0861412541 - 03474752361

Antonio Bernardo