Concetti Chiave
- Il modello AR(1) presenta un coefficiente ar1 di 0.6512 con un errore standard di 0.0578, ma non descrive bene i dati reali poiché il p-value non è sempre superiore a 0.5.
- Il modello AR(2) fornisce coefficienti ar1 e ar2 rispettivamente di 0.0527 e -0.0252, ma anch'esso non rappresenta accuratamente i dati reali, con p-value spesso inferiore a 0.5.
- Nel modello MA(1), il coefficiente ma1 è pari a -0.5363 con un errore standard di 0.0755, e il modello non rispecchia adeguatamente i dati reali a causa del p-value basso.
- Il modello ARIMA (1,1,1) include i coefficienti ar1 e ma1 di -0.0405 e 0.4255 rispettivamente, mostrando un buon adattamento ai dati grazie a un p-value sempre sopra 0.5.
- La stima della varianza sigma^2 per i diversi modelli varia, con il modello ARIMA che mostra una stima di 0.9271 e un AIC di 475.74, suggerendo un miglior adattamento rispetto ad altri modelli.
> ar1fit> ar1fit
Call:
arima(x = ar1, order = c(1, 1, 0), include.mean = FALSE)
Coefficients:
ar1
0.6512
s.e. 0.0578
sigma^2 estimated as 0.9409: log likelihood = -236.31, aic = 476.63
> tsdiag(ar1fit)
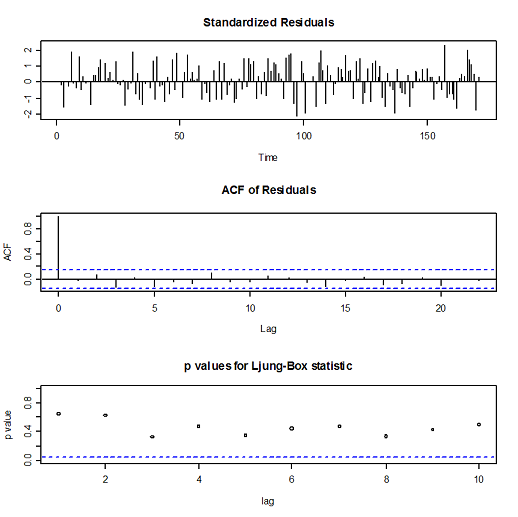
Poiché il p- value non è sempre superiore a 0,5 allora il processo non descrive bene i dati reali.
Stima dei parametri ar2
> ar22fit> ar22fit
Call:
arima(x = ar22, order = c(2, 1, 0), include.mean = FALSE)
Coefficients:
ar1 ar2
0.0527 -0.0252
s.e.
0.0768 0.0767
sigma^2 estimated as 0.1816: log likelihood = -95.65, aic = 197.3
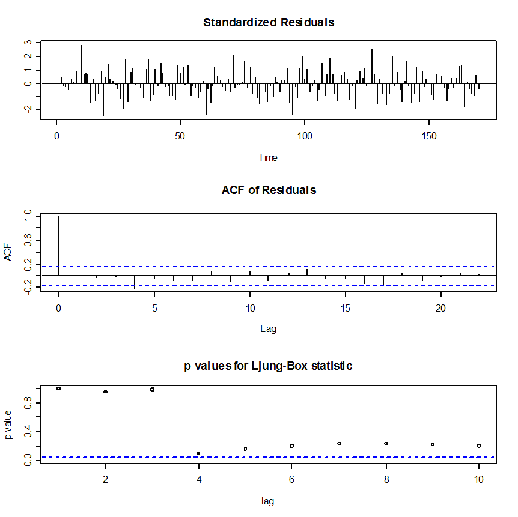
> tsdiag(ar22fit)
Anche in questo caso il p- value non è sempre superiore a 0,5 allora il processo non descrive bene i dati reali.
Stima dei parametri ma1
> fitma1> fitma1
Call:
arima(x = ma1, order = c(0, 1, 1))
Coefficients:
ma1
-0.5363
s.e. 0.0755
sigma^2 estimated as 0.8968: log likelihood = -232.14, aic = 468.27
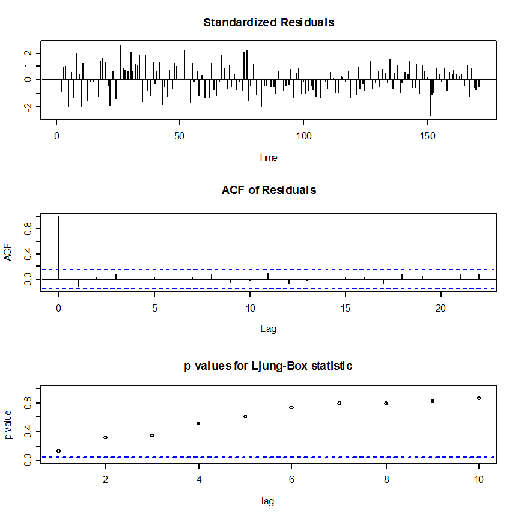
> tsdiag(fitma1)
Anche in questo caso il p- value non è sempre superiore a 0,5 allora il processo non descrive bene i dati reali.
Stima dei parametri ARIMA
> arimafit> arimafit
Call:
arima(x = arima1, order = c(1, 1, 1), include.mean = FALSE)
Coefficients:
ar1 ma1
-0.0405 0.4255
s.e. 0.2204 0.2044
sigma^2 estimated as 0.9271: log likelihood = -234.87, aic = 475.74
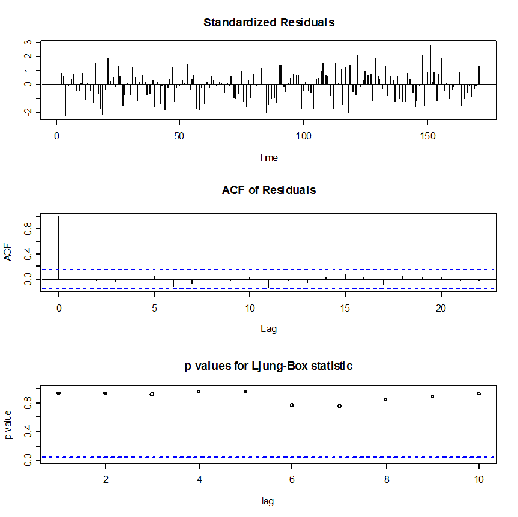
> tsdiag(arimafit)
Poiché il p- value si mantiene sempre al di sopra della soglia dello 0,5 allora il modello ARIMA descrive in modo efficiente la nostra serie.
Accedi a tutti gli appunti
Tutor AI: studia meglio e in meno tempo
