Concetti Chiave
- Mathcad is used to study geometric transformations, specifically isometries applied to plane figures.
- Isometries consist of three types of elementary transformations: translations, rotations around the origin, and symmetries relative to the x-axis.
- Translations of a polygon involve adding a complex number to each component of a complex vector representing the polygon's vertices.
- Rotating a polygon by an angle around the origin is achieved by multiplying the complex vector by the angle.
- For symmetry about the x-axis, the conjugates of the complex numbers representing the polygon's vertices are considered.
In questa sezione mostreremo l'uso di Mathcad nello studio delle trasformazioni geometriche applicate alle figure piane. In particolare, vedremo le isometrie applicate ai movimenti rigidi delle figure piane. Useremo degli esempi per illustrare tali concetti.
Ogni isometria può essere considerata composta da tre tipi di trasformazioni elementari: Traslazioni, Rotazioni intorno all'origine e Simmetrie rispetto all'asse x .
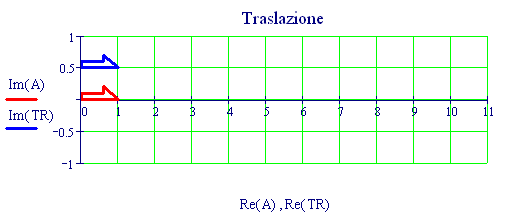
La Traslazione di un poligono, i cui vertici sono rappresentati da un vettore complesso, si può ottenere come somma di un vettore complesso e di un numero complesso. Mathcad si rivela molto utile nel sommare un numero complesso ad un vettore in quanto somma ad ogni componente del vettore il numero dato. Per R uotare un poligono di un angolo v intorno all'origine basta moltiplicare il vettore complesso, i cui elementi rappresentano i vertici del poligono, per v. Per la simmetria di un vettore A rispetto all'asse x basta considerare i complessi coniugati dei vertici del poligono dato.
Per vedere l'animazione clicca sul grafico seguente
In questa sezione mostreremo l'uso di Mathcad nello studio delle trasformazioni geometriche applicate alle figure piane. In particolare, vedremo le isometrie applicate ai movimenti rigidi delle figure piane. Useremo degli esempi per illustrare tali concetti.
Ogni isometria può essere considerata composta da tre tipi di trasformazioni elementari: Traslazioni, Rotazioni intorno all'origine e Simmetrie rispetto all'asse x .
La Traslazione di un poligono, i cui vertici sono rappresentati da un vettore complesso, si può ottenere come somma di un vettore complesso e di un numero complesso. Mathcad si rivela molto utile nel sommare un numero complesso ad un vettore in quanto somma ad ogni componente del vettore il numero dato. Per R uotare un poligono di un angolo v intorno all'origine basta moltiplicare il vettore complesso, i cui elementi rappresentano i vertici del poligono, per v. Per la simmetria di un vettore A rispetto all'asse x basta considerare i complessi coniugati dei vertici del poligono dato.
Per vedere l'animazione clicca sul grafico seguente
Per le rotazioni intorno all'origine del poligono individuato dal vettore A si procede nel modo seguente:
Per vedere l'animazione clicca sul grafico seguente
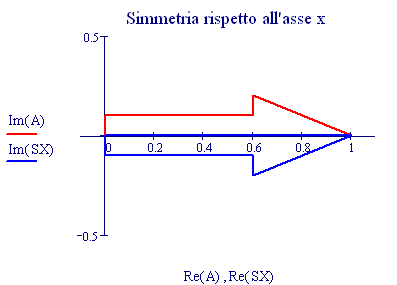
Per la simmetria rispetto all'asse x basta considerare il vettore avente come elementi i complessi coniugati degli elementi del vettore A . Pertanto basta considerare il seguente vettore e rappresentarlo
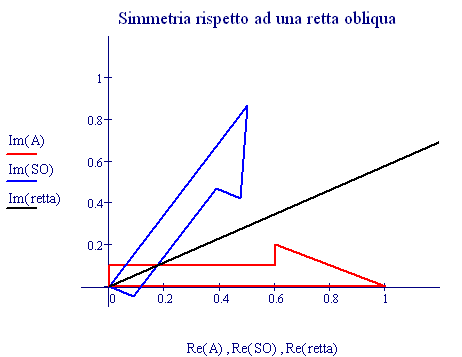
Per la simmetria rispetto ad una retta obliqua, passante per l'origine, basta considerare la trasformazione seguente:
Per una simmetria rispetto ad una retta, passante per l'origine degli assi ed inclinata di 30 gradi rispetto all'asse x, bisogna considerare i vettori seguenti :
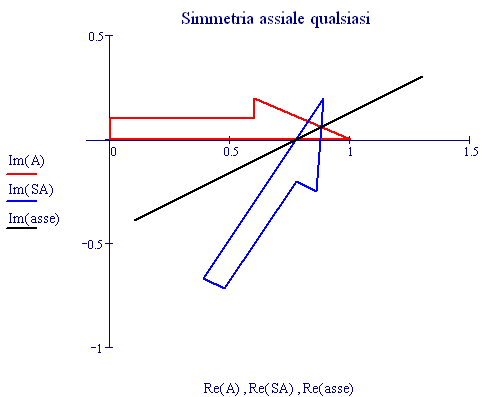
Per la simmetria rispetto ad una retta obliqua qualsiasi, non passante per l'origine, basta considerare la trasformazione seguente:
Per una simmetria rispetto ad una retta, non passante per l'origine degli assi ed inclinata di 30 gradi rispetto all'asse x, bisogna considerare i vettori seguenti:
Per le rotazioni intorno all'origine del poligono individuato dal vettore A si procede nel modo seguente:
Per vedere l'animazione clicca sul grafico seguente
Per la simmetria rispetto all'asse x basta considerare il vettore avente come elementi i complessi coniugati degli elementi del vettore A . Pertanto basta considerare il seguente vettore e rappresentarlo
Per la simmetria rispetto ad una retta obliqua, passante per l'origine, basta considerare la trasformazione seguente:
Per una simmetria rispetto ad una retta, passante per l'origine degli assi ed inclinata di 30 gradi rispetto all'asse x, bisogna considerare i vettori seguenti :
Per la simmetria rispetto ad una retta obliqua qualsiasi, non passante per l'origine, basta considerare la trasformazione seguente:
[url=https://www.skuola.net/informatica/isometrie-piane.html]
Per una simmetria rispetto ad una retta, non passante per l'origine degli assi ed inclinata di 30 gradi rispetto all'asse x, bisogna considerare i vettori seguenti:
Domande da interrogazione
- Quali sono i tre tipi di trasformazioni elementari che compongono un'isometria piana?
- Come si esegue una traslazione di un poligono utilizzando Mathcad?
- In che modo si effettua una rotazione di un poligono intorno all'origine?
- Come si realizza la simmetria di un vettore rispetto all'asse x?
- Qual è il procedimento per ottenere una simmetria rispetto a una retta obliqua non passante per l'origine?
Le isometrie piane sono composte da traslazioni, rotazioni intorno all'origine e simmetrie rispetto all'asse x.
La traslazione di un poligono si ottiene sommando un vettore complesso, che rappresenta i vertici del poligono, con un numero complesso.
Per ruotare un poligono di un angolo v intorno all'origine, si moltiplica il vettore complesso dei vertici del poligono per v.
La simmetria rispetto all'asse x si ottiene considerando i complessi coniugati dei vertici del poligono dato.
Per una simmetria rispetto a una retta obliqua non passante per l'origine, si deve considerare una specifica trasformazione dei vettori.







 Accedi a tutti gli appunti
Accedi a tutti gli appunti
 Tutor AI: studia meglio e in meno tempo
Tutor AI: studia meglio e in meno tempo