Concetti Chiave
- Il testo descrive come animare una curva variando l'angolo formato dalla linea tra l'origine e il centro del cerchio mobile.
- Viene utilizzata l'equazione del cerchio per disegnare il cerchio mobile in qualsiasi posizione, mostrando la curva tracciata da un punto su di esso.
- La Cardioide è generata da un punto su un cerchio che rotola su un altro cerchio di pari raggio, ed è un caso particolare dell'Epicicloide.
- Le equazioni parametriche sono impiegate per modellare il movimento e la posizione del cerchio fisso e quello mobile.
- Mathcad è lo strumento usato per inserire testo, equazioni e grafici, consentendo l'animazione della Cardioide tramite specifiche toolbar.
dove l'angolo formato dalla linea che congiunge l'origine con il centro del cerchio mobile e l'asse . La curva sar:
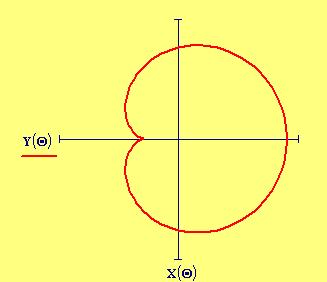
Ci piacerebbe animare il disegno della curva facendo in modo che l'angolo vari. Abbiamo bisogno di poter disegnare il cerchio ruotante in qualsiasi posizione .
In tale posizione il nostro cerchio avr centro:
Usando l'equazione del cerchio
troviamo due funzioni che possono essere usate per disegnare il nostro cerchio in una posizione qualsiasi
Cambiando il valore di , qui sotto, puoi vedere la nuova posizione del cerchio e la curva tracciata dal punto solidale ad esso. (Tutti gli angoli sono misurati in radianti.)
Ripetiamo l'impostazione data usando la variabile k come parametro per far variare l'angolo .
Per vedere l'animazione sulla Cardioide clicca sull'icona a lato
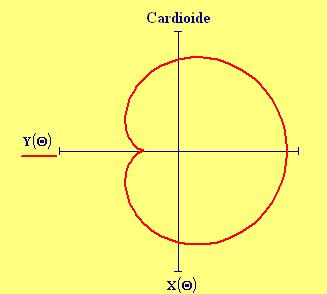
Una particolare Epicicloide animata con Mathcad: la Cardioide (Carlo Elce)
Nota
Per inserire del testo con Mathcad basta digitare da tastiera i caratteri che compongono le parole da riportare.
Per le equazioni bisogna avvalersi dellaToolbar Calculator o della Evaluation Toolbar, per i grafici della Toolbar Graph, per le lettere greche della Greek Symbol Toolbar, ed infine, per l'animazione, dal menu a discesa View cliccare sul pulsante Animate.
Nel file tutto ci che compare di colore blu o bordeaux testo puro semplice, mentre tutto ci che appare evidenziato in giallo stato digitato mediante le Toolbars di cui sopra.
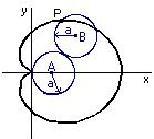
Le curve nel piano sono descritte spesso come punti che si muovono sottoposti a certe condizioni. Per esempio, la Cardioide generata da un punto P sulla circonferenza di un cerchio A che rotola su un altro cerchio B avente lo stesso raggio a. Essa un caso particolare dell'Epicicloide in quanto si ottiene da essa imponendo che i raggi dei due cerchi siano uguali tra loro.
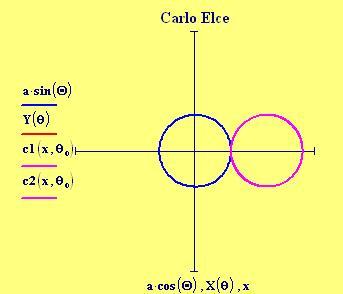
Incominciamo col disegnare due cerchi di raggio a e b tangenti esternamente con a=b.
raggi dei due cerchi
Useremo le equazioni parametriche in funzione di per disegnare il cerchio fisso,
ed per quello mobile
equazioni parametriche del cerchio fisso
equazioni dei due rami del cerchio mobile
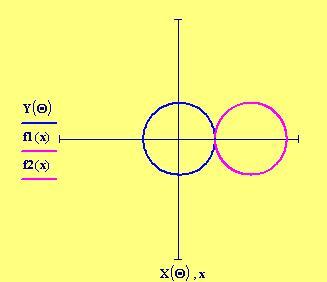
Il cerchio mobile inizia a rotolare in senso antiorario lungo la circonferenza del cerchio fisso. Se teniamo il nostro occhio fermo su di un punto della circonferenza solidale al cerchio mobile, vediamo che esso traccia una curva man mano che il cerchio rotola partendo dal punto
Metteremo a punto un'animazione che ci mostrer la curva descritta dal punto solidale al cerchio ruotante.
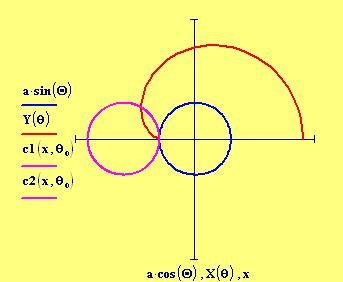
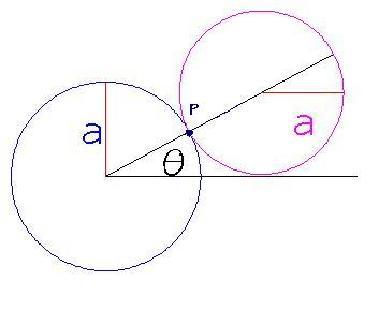
Con un p di trigonometria ed il disegno qui sotto,
possiamo trovare le equazioni parametriche per la curva tracciata dal punto solidale al cerchio mobile;
dove l'angolo formato dalla linea che congiunge l'origine con il centro del cerchio mobile e l'asse . La curva sar:

Ci piacerebbe animare il disegno della curva facendo in modo che l'angolo vari. Abbiamo bisogno di poter disegnare il cerchio ruotante in qualsiasi posizione .
In tale posizione il nostro cerchio avr centro:
Usando l'equazione del cerchio
troviamo due funzioni che possono essere usate per disegnare il nostro cerchio in una posizione qualsiasi
Cambiando il valore di , qui sotto, puoi vedere la nuova posizione del cerchio e la curva tracciata dal punto solidale ad esso. (Tutti gli angoli sono misurati in radianti.)
Ripetiamo l'impostazione data usando la variabile k come parametro per far variare l'angolo .
Per vedere l'animazione sulla Cardioide clicca sull'icona a lato

Una particolare Epicicloide animata con Mathcad: la Cardioide (Carlo Elce)
Nota
Per inserire del testo con Mathcad basta digitare da tastiera i caratteri che compongono le parole da riportare.
Per le equazioni bisogna avvalersi dellaToolbar Calculator o della Evaluation Toolbar, per i grafici della Toolbar Graph, per le lettere greche della Greek Symbol Toolbar, ed infine, per l'animazione, dal menu a discesa View cliccare sul pulsante Animate.
Nel file tutto ci che compare di colore blu o bordeaux testo puro semplice, mentre tutto ci che appare evidenziato in giallo stato digitato mediante le Toolbars di cui sopra.
Le curve nel piano sono descritte spesso come punti che si muovono sottoposti a certe condizioni. Per esempio, la Cardioide generata da un punto P sulla circonferenza di un cerchio A che rotola su un altro cerchio B avente lo stesso raggio a. Essa un caso particolare dell'Epicicloide in quanto si ottiene da essa imponendo che i raggi dei due cerchi siano uguali tra loro.
Incominciamo col disegnare due cerchi di raggio a e b tangenti esternamente con a=b.
raggi dei due cerchi
Useremo le equazioni parametriche in funzione di per disegnare il cerchio fisso,
ed per quello mobile
equazioni parametriche del cerchio fisso
equazioni dei due rami del cerchio mobile
Il cerchio mobile inizia a rotolare in senso antiorario lungo la circonferenza del cerchio fisso. Se teniamo il nostro occhio fermo su di un punto della circonferenza solidale al cerchio mobile, vediamo che esso traccia una curva man mano che il cerchio rotola partendo dal punto
Metteremo a punto un'animazione che ci mostrer la curva descritta dal punto solidale al cerchio ruotante.
Con un p di trigonometria ed il disegno qui sotto,
possiamo trovare le equazioni parametriche per la curva tracciata dal punto solidale al cerchio mobile;
Domande da interrogazione
- Qual è il concetto principale descritto nel testo?
- Come si può animare la Cardioide utilizzando Mathcad?
- Quali strumenti di Mathcad sono necessari per creare l'animazione?
- Qual è la relazione tra la Cardioide e l'Epicicloide?
- Qual è il ruolo delle equazioni parametriche nel disegno della curva?
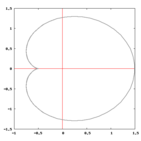
Il testo descrive la generazione e l'animazione di una curva chiamata Cardioide, creata da un punto su un cerchio che rotola su un altro cerchio di uguale raggio.
Per animare la Cardioide in Mathcad, si utilizza la variabile k come parametro per variare l'angolo, e si sfruttano le diverse toolbar per inserire testo, equazioni e grafici.
Sono necessari la Toolbar Calculator, la Evaluation Toolbar, la Toolbar Graph, la Greek Symbol Toolbar e il menu a discesa View per l'animazione.
La Cardioide è un caso particolare dell'Epicicloide, ottenuta quando i raggi dei due cerchi coinvolti sono uguali.
Le equazioni parametriche sono utilizzate per disegnare sia il cerchio fisso che quello mobile, permettendo di tracciare la curva generata dal punto solidale al cerchio mobile.






 Accedi a tutti gli appunti
Accedi a tutti gli appunti
 Tutor AI: studia meglio e in meno tempo
Tutor AI: studia meglio e in meno tempo