Concetti Chiave
- La legge dei gas perfetti combina le leggi di Boyle, Charles e Gay-Lussac per descrivere il comportamento dei gas ideali.
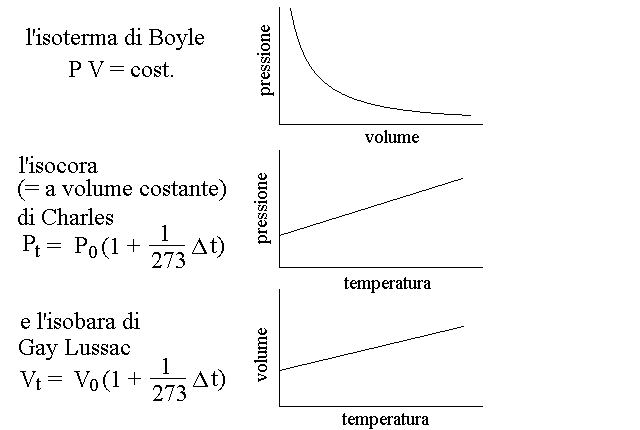
- La legge di Boyle si applica quando la temperatura è costante, rappresentando il prodotto pressione-volume come costante.
- La legge di Charles descrive variazioni di pressione con temperatura costante quando il volume è inalterato, risultando in una rappresentazione lineare.
- La legge di Gay-Lussac riguarda cambiamenti di volume con pressione costante quando la temperatura varia, visualizzabile come una linea retta.
- L'equazione generale dei gas ideali è
PV=nRT, doveRè la costante dei gas perfetti; per molecole, si usaPV=k_B NTcon la costante di Boltzmannk_B.
LEGGE DEI GAS PERFETTI
Una breve parentesi sulle formule precedenti applicate ai gas;
SE LA TEMPERATURA E' COSTANTE VARIANO P E V,QUINDI:
(legge di Boyle) rappresentato graficamente con ramo di iperbole detto isoterma
SE IL VOLUME E' COSTANTE VARIANO T E P,QUINDI:
(Legge di Charles), con
rispettivamente la pressione allo stato iniziale e la variazione di temperatura,
una costante specifica per il gas, e si rappresenta graficamente con una retta che si chiama isocora.
SE LA PRESSIONE E' COSTANTE VARIANO T E V, QUINDI:
(legge di Gay Lussac), con
rispettivamente il volume allo stato iniziale e la variazione di temperatura,
una costante specifica per il gas, si rappresenta sempre con una retta definita isobara.
Detto cio' la legge dei gas perfetti si ricava COMBINANDO QUESTE 3 LEGGI sopra illustrate. Si parte da condizioni note, quindi si suppone di avere una mole di gas (perfetto) alle seguenti condizioni
(con unità di misura, rispettivamente, di atmosfera, grado centigrado e litri). Si sottopone quindi il gas ad un ciclo di trasformazioni descritte in precedenza. Le trasformazioni vanno dal punto
al punto
tramite una trasformazione isobara, e dal punto
al punto
tramite una trasformazione isoterma.
1) Da
a
noterete che la pressione resta la stessa (
), quindi si applica la terza legge sopra esposta che vale appunto quando la pressione è costante: nel punto
quindi
.
2) Dal punto
al punto
resta invece costante la temperatura, quindi graficamente vedete il ramo di iperbole ed è applicabile la legge di Boyle per cui
. La costante, in questo caso, è rappresentata dal prodotto di
, i valori di pressione e volume nel punto
, quindi sostituendo a “costante” i valori summenzionati:
Pertanto si ha, nella trasformazione da
a
QUESTA DA SOLA SAREBBE GIA' L'EQUAZIONE DI STATO DEI GAS IDEALI, ma va “arricchita”. Si vogliono usare i gradi Kelvin, quindi t, temperatura celsius, va divisa per 273:
e dal momento che per la temperatura espressa in Kelvin si ha la relazione
Ma
è una quantità costante nota (perché sono le nostre condizioni iniziali), e dai valori scritti in precedenza si ricava
Questa costante viene detta costante dei gas perfetti. Abbiamo quindi, per una quantità 1 molare di gas la legge
Dal momento che, in generale, si lavora con gas con
moli, tale legge viene modificata nella forma più generale
la quale prende il nome di legge dei gas perfetti. Nel caso, invece, si voglia lavorare con le molecole presenti nel gas, indicato con
il numero di tali molecole si ha la relazione
dove
è il numero di Avogadro. Sostituendo l'espressione
nella legge precedente otteniamo
dove la quantità
è detta costante di Boltzman.
Domande da interrogazione
- Qual è la legge di Boyle e come si rappresenta graficamente?
- Come si applica la legge di Charles e quale grafico la rappresenta?
- Cosa descrive la legge di Gay Lussac e come viene rappresentata?
- Come si ricava l'equazione di stato dei gas ideali?
- Qual è la relazione tra il numero di molecole e la costante di Boltzmann?
La legge di Boyle afferma che il prodotto della pressione e del volume di un gas è costante a temperatura costante, rappresentato graficamente con un ramo di iperbole detto isoterma.
La legge di Charles si applica quando il volume è costante e varia la temperatura e la pressione, rappresentata graficamente con una retta chiamata isocora.
La legge di Gay Lussac descrive la relazione tra volume e temperatura a pressione costante, rappresentata graficamente con una retta definita isobara.
L'equazione di stato dei gas ideali si ricava combinando le leggi di Boyle, Charles e Gay Lussac, e si esprime come \(PV=nRT\), dove \(R\) è la costante dei gas perfetti.
La relazione è data da \(PV=\frac{R}{N_A} NT=k_B N T\), dove \(k_B\) è la costante di Boltzmann, e \(N\) è il numero di molecole del gas.
Accedi a tutti gli appunti
Tutor AI: studia meglio e in meno tempo
