Meccanica: Un carrello da supermercato di massa 10,0 kg viene spinto per 2,00 m da fermo con una forza di 100 N . La forza di attrito con il pavimento è di 30,0 N....

di _francesca.ricci

Ominide

2 min. di lettura

Vota

Concetti Chiave

Il lavoro compiuto dalla forza applicata al carrello è di 200 Joule, ottenuto moltiplicando la forza per lo spostamento.
La forza di attrito compie un lavoro negativo di -60 Joule, poiché si oppone al movimento del carrello.
Il lavoro totale, somma dei lavori parziali, è di 140 Joule, determinando la variazione di energia cinetica.
Il carrello parte da fermo, quindi la sua velocità iniziale e l'energia cinetica iniziale sono entrambe nulle.
La velocità finale del carrello, calcolata dalla variazione di energia cinetica, è di 5,29 m/s.

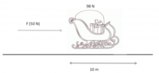
Un carrello da supermercato di massa

[math]10,0 kg[/math]

viene spinto per

[math]2,00 m[/math]

da fermo con una forza di

[math]100 N[/math]

. La forza di attrito con il pavimento è di

[math]30,0 N[/math]

Quanto vale il lavoro compiuto dalla forza applicata al carrello?
Quanto vale il lavoro compiuto dalla forza di attrito?
Qual è la velocità finale del carrello?

Svolgimento (1)

Calcoliamo il lavoro compiuto dalla forza applicata al carrello moltiplicando il valore della forza per lo spostamento.

Poiché lo spostamento ha lo stesso verso della forza, il lavoro compiuto sarà positivo:

[math] L = F \cdot S = 100N \cdot 2,00 m = 200 J [/math]

Svolgimento (2)

Il lavoro compiuto dalla forza di attrito è un lavoro negativo, poiché la forza so oppone allo spostamento:

[math] L_a = - F \cdot S = - 30,0 N \cdot 2,00 m = - 60 J [/math]

Svolgimento (3)

Per determinare la velocità finale del carrello consideriamo il lavoro totale svolto dallo stesso. Il lavoro totale è dato dalla variazione di energia cinetica:

[math] L = âˆ†k = k_f - k_i = 1/2 m v_f ^2 - 1/2 m v_i ^2 [/math]

Sapendo che il carrello parte da fermo, possiamo affermare che la sua velocità iniziale è nulla, di conseguenza sarà nulla anche la sua energia cinetica iniziale:

[math] L = âˆ†k = k_f - 0 = k_f [/math]

Sapendo che il lavoro totale è dato dalla somma dei lavori parziali, determiniamo il lavoro totale:

[math] L_(TOT) = L + L_a = 200 J - 60 J = 140 J [/math]

Poiché il lavoro totale è uguale all'energia cinetica finale, impostiamo che

[math] k_f = 1/2 m v_f ^2 = 140 J [/math]

e ricaviamo la velocità finale:

[math] k_f = 1/2 m v_f ^2 \to v_f ^2 = frac(2k_f)(m) \to v_f = \sqrt{frac(2k_f)(m)} [/math]

[math] v = \sqrt{frac(2 \cdot 140 J)(10,0 kg)} = 5,29 m/s [/math]

Domande da interrogazione

Qual è il lavoro compiuto dalla forza applicata al carrello?

Il lavoro compiuto dalla forza applicata al carrello è di 200 J, calcolato moltiplicando la forza di 100 N per lo spostamento di 2,00 m.

Quanto vale il lavoro compiuto dalla forza di attrito?

Il lavoro compiuto dalla forza di attrito è di -60 J, poiché la forza di attrito di 30,0 N si oppone allo spostamento di 2,00 m.

Qual è la velocità finale del carrello?

La velocità finale del carrello è 5,29 m/s, determinata considerando il lavoro totale di 140 J e la massa del carrello di 10,0 kg.

Meccanica: Un carrello da supermercato di massa 10,0 kg viene spinto per 2,00 m da fermo con una forza di 100 N . La forza di attrito con il pavimento è di 30,0 N....

Esercizio di meccanica: lavoro e forza di attrito, calcolo della velocità finale di un corpo in movimento sottoposto alla forza di attrito