Concetti Chiave
- Il circuito è analizzato per determinare il verso e l'intensità della corrente attraverso una batteria da 12 V, utilizzando le leggi di Kirchhoff.
- Le resistenze nel circuito sono date come R1 = 16 Ω, R2 = 25 Ω e R3 = 18 Ω, con differenze di potenziale V1 = 18 V e V2 = 12 V.
- La legge dei nodi di Kirchhoff afferma che la somma delle correnti entranti in un nodo è uguale alla somma delle correnti uscenti, indicato come i2 + i3 = i1.
- L'applicazione della legge delle maglie porta a due equazioni principali, risolvendo le quali si trova i2 = -6/41 A e i3 = 2/3 A.
- La corrente i1, che attraversa il generatore, è calcolata come i1 = 0,52 A, indicando che il verso è da A a B.
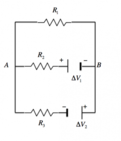
In questo appunto andremo a studiare la struttura di un circuito, cercando di determinare verso e intensità della corrente che attraversa un generatore. Per fare ciò utilizzeremo le leggi di Kirchhoff in maniera opportuna. Vediamo il testo dell'esercizio.
Testo dell'esercizio
Determina verso e intensità della corrente che attraversa la batteria da
Sono forniti i seguenti valori delle resistenze:
. E delle differenze di potenziale:
.
Svolgimento dell'esercizio
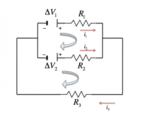
Per risolvere il circuito e determinare verso e intensità delle correnti dobbiamo ricorrere alle leggi di Kirchhoff, poiché abbiamo due generatori di tensione.
Per prima cosa, scegliamo dei versi di percorrenza delle maglie e diamo alle correnti dei versi arbitrari: se poi la corrente sarà positiva il verso da noi scelto è quello giusto, altrimenti il verso giusto è il contrario.
Applichiamo la legge dei nodi, per cui la somma delle correnti entranti in un nodo è uguale alla somma delle correnti che escono:
Applichiamo poi per le due maglie scelte la legge delle maglie, per cui la somma algebrica delle differenze di potenziale che si incontrano percorrendo una maglia è uguale a zero.
Per la prima maglia abbiamo:
Per la seconda maglia:
Mettiamo a sistema le tre equazioni:
i_2 = -\frac{6}{41} A \\
i_3 = \frac{2}{3} A
\end{cases} [/math]
Possiamo ora determinare il valore della corrente che attraversa il generatore richiesto:
E dato che essa è positiva, il suo verso è proprio quello da A a B.
Domande da interrogazione
- Qual è il metodo utilizzato per determinare verso e intensità della corrente nel circuito?
- Quali sono i valori delle resistenze e delle differenze di potenziale forniti nell'esercizio?
- Qual è il risultato finale per la corrente che attraversa il generatore richiesto?
Per determinare verso e intensità della corrente nel circuito, si utilizzano le leggi di Kirchhoff, applicando la legge dei nodi e la legge delle maglie.
I valori delle resistenze sono [math] R_1 = 16 \Omega , R_2 = 25 \Omega , R_3 = 18 \Omega [/math], mentre le differenze di potenziale sono [math] V_1 = 18 V , V_2 = 12 V [/math].
La corrente che attraversa il generatore richiesto è [math] i_1 = 0,52 A [/math] e il suo verso è da A a B, poiché il valore è positivo.
Accedi a tutti gli appunti
Tutor AI: studia meglio e in meno tempo
