Concetti Chiave
- L'esercizio richiede di calcolare il campo elettrico risultante in un punto, considerando due cariche puntiformi disposte in un triangolo rettangolo.
- Il campo elettrico generato da ciascuna carica viene calcolato usando la formula di Coulomb, tenendo conto delle distanze specifiche.
- I campi elettrici di entrambe le cariche sono perpendicolari, quindi il campo risultante viene determinato applicando il teorema di Pitagora.
- Il valore del campo elettrico risultante, senza la presenza di un mezzo dielettrico, è calcolato come 7,5 × 10^7 N/C.
- In presenza di un mezzo con costante dielettrica relativa di 2,5, il campo elettrico risultante si riduce a 3 × 10^7 N/C.
Questo appunto si propone di risolvere un esercizio in cui viene richiesto di trovare il campo elettrico in un punto del piano, facendo attenzione al fatto che le cariche hanno una disposizione particolare. Bisognerà infatti ricordare che, dato che abbiamo a che fare con un triangolo rettangolo, i vettori campo elettrico andranno sommati opportunamente, tenendo conto del Teorema di Pitagora. Vediamo ora il testo dell'esercizio.
Testo dell'esercizio
Due cariche puntiformi
e
sono disposte come nella figura. Calcola il campo elettrico risultante nel punto
.
Se invece le due cariche fossero immerse in un mezzo di costante dielettrica relativa
, quale sarebbe il valore del campo in
?
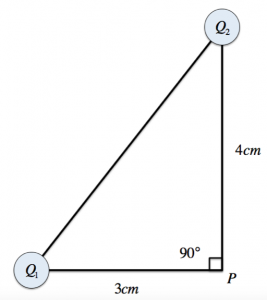
Svolgimento parte 1
Il campo elettrico creato da
è descritto dalla nota formula
e vale:
Allo stesso modo, il campo creato da
risulta:
Poiché i due campi sono perpendicolari calcoliamo il campo risultante con il teorema di Pitagora:
Svolgimento parte 2
Se le due cariche fossero in un mezzo dielettrico di costante
, il campo sarebbe
volte minore; quindi sarebbe:
Accedi a tutti gli appunti
Tutor AI: studia meglio e in meno tempo
