Concetti Chiave
- Il calcolo del moto di un satellite utilizza il metodo di Runge-Kutta del quarto ordine.
- Due casi di orbite vengono esaminati: una circolare e una ellittica, determinate dalla velocità iniziale.
- La forza gravitazionale varia inversamente con il quadrato della distanza dal centro del campo.
- Le equazioni differenziali descrivono il moto del pianeta sotto l'influenza di un campo gravitazionale centrale.
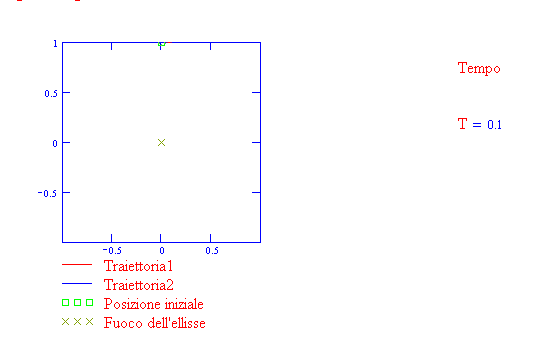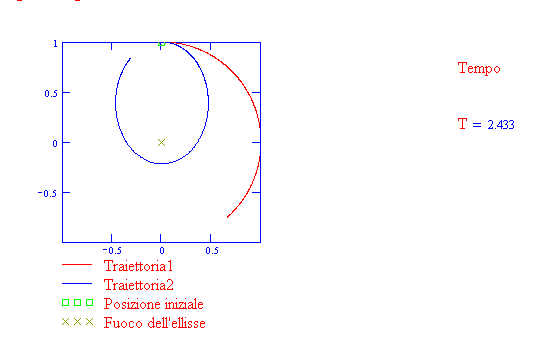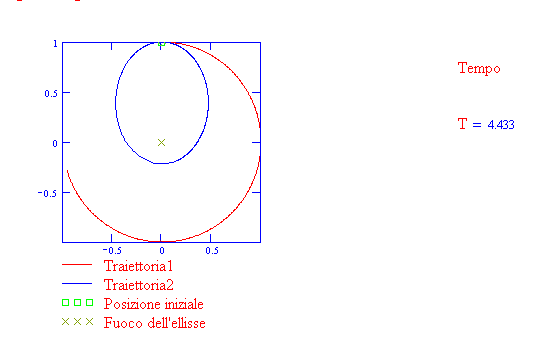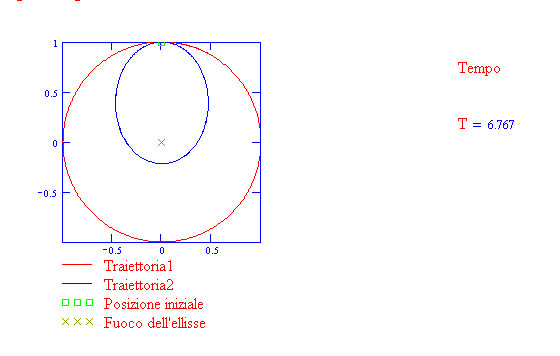
- La traiettoria risulta ellittica quando sottoposta a un campo gravitazionale diretto verso un fuoco, secondo la prima legge di Kepler.
In questa sezione illustreremo il calcolo per trovare il moto di un satellite, a partire dalla posizione e dalla velocità iniziale, e useremo il metodo di Runge-Kutta del quarto ordine. 
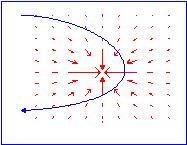
Esamineremo due casi: uno il cui risultato è un'orbita circolare, l'altro , la cui velocità iniziale è minore rispetto alla prima, da come risultato un'orbita ellittica.
La forza dovuta al campo gravitazionale varia in modo inversamente proporzionale al quadrato della distanza dalla sorgente del campo. Pertanto le equazioni differenziali per il moto del pianeta sono:
| Originale | Perturbazione | |
| posizione iniziale rispetto a x : | 
|
 |
| posizione iniziale rispetto a y : |
|
 |
| velocità iniziale in direzione x : |
|
|
| velocità iniziale in direzione y: |
|
|
tempo: 
La traiettoria è un'ellisse se il pianeta è sottoposto ad un campo gravitazionale centrale diretto
verso il fuoco (prima legge di Kepler). Osserva la seguente animazione
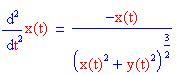
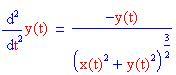
Accedi a tutti gli appunti
Tutor AI: studia meglio e in meno tempo
