Concetti Chiave
- L'iterazione di una funzione implica la valutazione ripetuta della funzione a partire da un valore iniziale chiamato seme.
- L'uscita di ogni iterazione della funzione forma un'orbita, che può mostrare diversi comportamenti a seconda del seme e della funzione stessa.
- Le orbite possono tendere a un punto fisso, all'infinito, essere periodiche o mostrare un comportamento caotico.
- Piccole variazioni nel parametro c di una funzione iterata possono causare grandi differenze nel comportamento dell'orbita.
- Il testo esplora come diverse funzioni e valori di c influenzano l'andamento delle orbite, con attenzione ai comportamenti caotici.
Valutazione di Funzioni
Iterazioni e orbite
Iterare una funzione significa valutare la funzione ripetutamente. Nella prima iterazione, la funzione è valutata per un valore iniziale (chiamato seme ). Nella seconda iterazione la funzione è valutata per il valore uscito dalla prima iterazione e così via.
La sequenza dei valori in uscita è chiamata orbita della funzione iterata per il seme assegnato.
Una delle cose meravigliose dell'era dei computer è che possiamo demandare agli elaboratori elettronici calcoli noiosi (come quelli delle iterazioni), che essi svolgono in una frazione di secondo.
Ecco una procedura che valuta una funzione iterata per un seme assegnato. Questa procedura usa una variabile intervallo e una variabile indice per mantenere la traccia delle successive iterazioni.
Reiteriamo la funzione per
.
troviamo la prima iterazione:
Impostiamo l'intervallo delle iterazioni da 2 a un dato valore n:
Reiteriamo la funzione e listiamo l'orbita:
Provate a cambiare il seme in 35, 88, e -10.
Quali risultati ci si può aspettare?
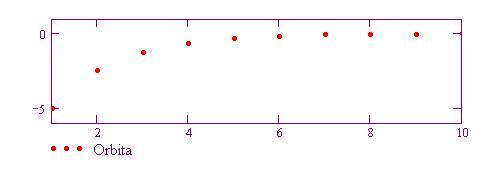
L'orbita è rappresentata qui sotto. Quale effetto produce il seme sull'andamento dell'orbita?
Provate ad iterare le seguenti funzioni:
A seconda della funzione da iterare e del valore per il seme scelto, si possono scoprire comportamenti molto diversi per l'orbita.
Ecco i comportamenti di diverse orbite.
punto fisso
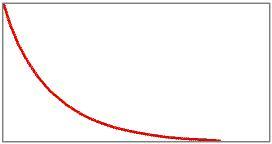
tende a un punto fisso
tende a un punto fisso
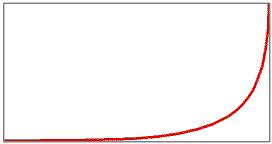
tende all'infinito
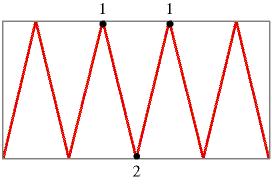
Qui l'orbita oscilla tra due valori ed è detta periodica con periodo 2.
periodica
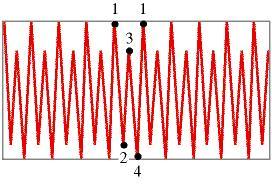
con periodo 4
periodica con
periodo 6
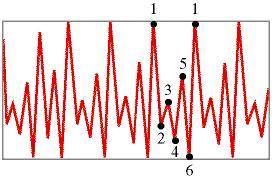
Qui non è riconoscibile alcuna struttura. Questo comportamento è detto caotico!
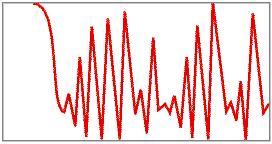
Anche sistemi dinamici semplici possono presentare un andamento imprevedibile o caotico. Qui sotto itereremo una famiglia di funzioni della forma f(x) = x 2 – c, per vedere come piccole variazioni del valore di c possono dare origine a comportamenti molto diversi.
Iterare la funzione per differenti valori di c (c è globalmente definito sotto), mantenendo costante il valore del seme
.
Prima iterazione:
Intervallo delle iterazioni:
Iterazione della funzione:
Provate a far variare c da 0.1 a 0.2, poi 0.3, poi 0.4, poi 0.5, e così via fino a 2. Notate il diverso comportamento delle orbite! Per ogni valore di c, rappresentate il tipo di comportamento mostrato.
lo facciamo noi per voi con il grafico di una funzione parametrica che presenta proprio c come parametro
Il grafico seguente fa vedere l'animazione sulla variazione dell'orbita
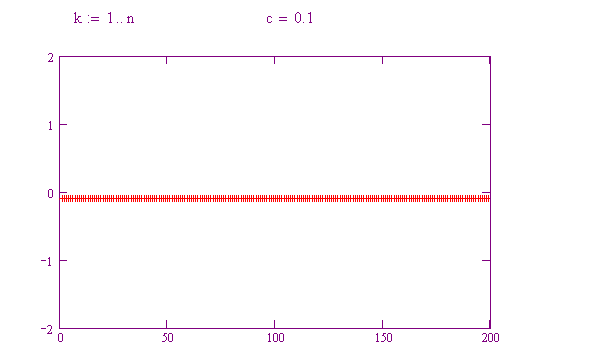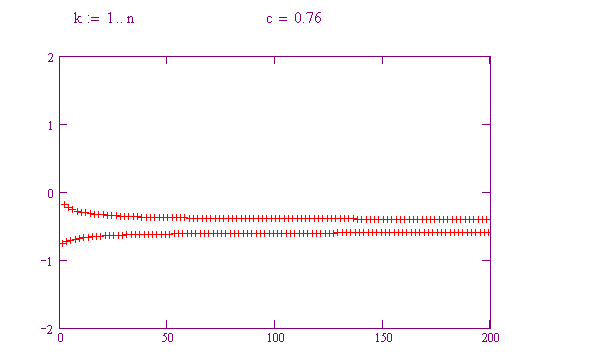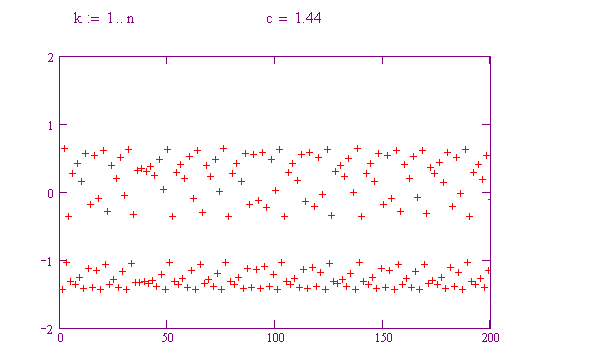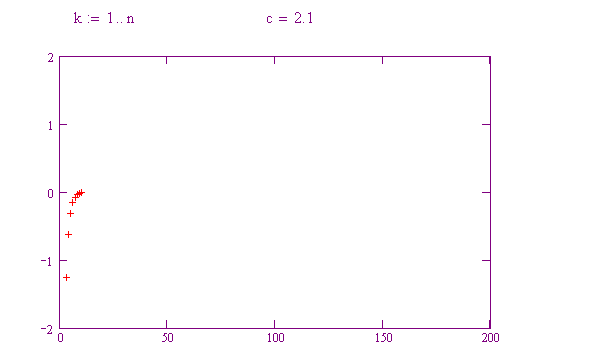
Per quali valori di c la funzione presenta un andamento caotico?
Domande da interrogazione
- Cosa significa iterare una funzione e qual è il ruolo del seme in questo processo?
- Quali tipi di comportamenti possono emergere dall'iterazione di una funzione?
- Come influiscono le variazioni del parametro c sul comportamento dell'orbita della funzione f(x) = x^2 - c?
Iterare una funzione significa valutarla ripetutamente, iniziando da un valore iniziale chiamato seme. Il seme determina l'andamento dell'orbita, che è la sequenza dei valori ottenuti dalle iterazioni.
A seconda della funzione e del seme scelto, l'orbita può tendere a un punto fisso, all'infinito, essere periodica o mostrare un comportamento caotico.
Piccole variazioni di c possono causare comportamenti molto diversi nell'orbita, che possono essere visualizzati tramite un grafico parametrico.

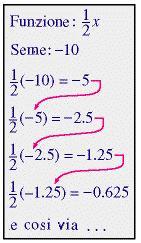








 Accedi a tutti gli appunti
Accedi a tutti gli appunti
 Tutor AI: studia meglio e in meno tempo
Tutor AI: studia meglio e in meno tempo