Concetti Chiave
- Le grandezze scalari si definiscono unicamente con un valore numerico e un'unità di misura, mentre quelle vettoriali richiedono anche la direzione.
- Un vettore è un segmento orientato caratterizzato da lunghezza, direzione e verso, essenziali per definirne l'orientamento nello spazio.
- Il metodo punta-coda è utilizzato per sommare vettori consecutivi, collegando la coda del primo alla punta del secondo.
- La regola del parallelogramma consiste nel costruire un parallelogramma con i due vettori come lati, utilizzando la diagonale come vettore risultante.
- Le componenti cartesiane di un vettore si trovano scomponendolo nel piano cartesiano, utilizzando il teorema di Pitagora per calcolare lunghezze e angoli.
Indice
Differenza tra grandezze scalari e vettoriali
-
Vettore = Il vettore3 è un segmento orientato, definito da tre caratteristiche fondamentali:
- 1.Lunghezza/ modulo/ intensità = Sono la distanza tra i due estremi del vettore, detto coda o primo estremo (l’inizio) e punta o secondo estremo (la fine).
- 2.Direzione = La direzione è quella individuata dalla retta a cui il vettore appartiene o anche da qualsiasi altra retta parallela ad esso. (infatti, rette parallele individuano la stessa direzione.)
- 3.Verso = Il verso ci permette di distinguere il primo dal secondo estremo del vettore, che per convenzione vengono chiamati rispettivamente estremo positivo ed estremo negativo.

ATTENZIONE! I vettori vengono indicati tramite una lettera posta sotto una freccia.
Metodo punta-coda
Se due vettori sono consecutivi e puntano anche nella stessa direzione, è possibile applicare la somma di due vettori sulla stessa retta, in modo semplice e veloce.
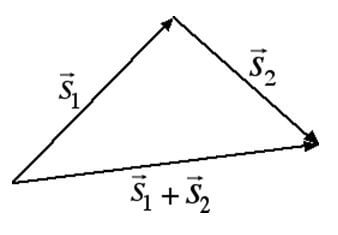
Quando, invece, si è in presenza di due vettori consecutivi, ma che puntano in direzioni diverse, va applicato il metodo punta-coda.
Metodo punta-coda = si unisce tramite un segmento orientato la coda del primo vettore con la punta del secondo vettore. Il modulo del segmento tracciato equivale alla somma dei due vettori. (Questo metodo si può applicare anche quando abbiamo più di due vettori.)
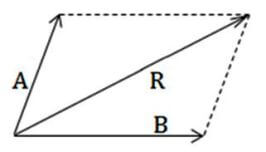
Regola del parallelogramma
Va costruito un parallelogramma che ha per lati i due vettori. In seguito, va tracciata una diagonale, passante per il punto O. Questa diagonale rappresenta il vettore finali (quindi un eventuale spostamento risultante).
-
Attenzione! Il metodo punta-coda e la regola del parallelogramma sono perfettamente equivalenti. Nonostante ciò, quando bisogna sommare più vettori, si consiglia principalmente il metodo punta-coda.
Componenti cartesiani di un vettore
Scomposizione del vettore = disegno del vettore sul piano cartesiano per trovare altri due (nel piano) vettori, la cui somma sia uguale al vettore dato.
Componenti di un vettore (vx e vy) = quantità scalari, seguiti da un’unità di misura. Hanno come valore il modulo dei vettori componenti e segno positivo o negativo a seconda del verso in cui sono orientati.
Essendo cateti di un triangolo rettangolo (di cui il vettore è l’ipotenusa), sodisfano il teorema di pitagora.
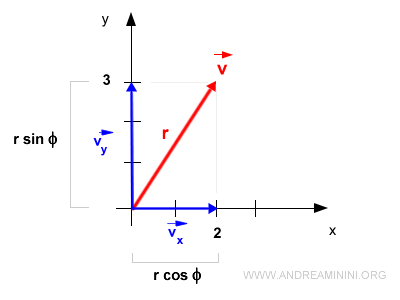
Per calcolare alcuni valori dell’angolo θ (che il vettore forma con l’asse delle x) bisogna usare seno (sin) e coseno (cos).
Un cateto è uguale al prodotto dell’ipotenusa per l’angolo.
Domande da interrogazione
- Qual è la principale differenza tra grandezze scalari e vettoriali?
- Cosa rappresenta un vettore e quali sono le sue caratteristiche fondamentali?
- Come si sommano due vettori che puntano in direzioni diverse?
- Come si calcolano i valori dell'angolo θ formato da un vettore con l'asse delle x?
Le grandezze scalari sono definite unicamente dal loro valore numerico e dall'unità di misura, mentre le grandezze vettoriali richiedono informazioni aggiuntive sulla direzione, espressa tramite un vettore.
Un vettore è rappresentato da un segmento orientato con tre caratteristiche fondamentali: lunghezza (o modulo), direzione e verso, che indicano rispettivamente la distanza tra i due estremi del vettore, la retta a cui appartiene e la distinzione tra l'estremo positivo e negativo.
Per sommare due vettori che puntano in direzioni diverse si applica il metodo punta-coda, unendo la coda del primo vettore con la punta del secondo tramite un segmento orientato, il cui modulo rappresenta la somma dei due vettori.
Per calcolare i valori dell'angolo θ si utilizzano il seno e il coseno, dove il coseno di θ è il rapporto tra il cateto adiacente all'angolo e l'ipotenusa, mentre il seno di θ è il rapporto tra il cateto opposto all'angolo e l'ipotenusa.






 Accedi a tutti gli appunti
Accedi a tutti gli appunti
 Tutor AI: studia meglio e in meno tempo
Tutor AI: studia meglio e in meno tempo