Esempio di quesito che solitamente i ragazzi si trovano ad affrontare durante i test d'ingresso per accedere all'università Bocconi. Ecco il metodo risolutivo di un problema di geometria analitica basato sulla più semplice delle funzioni: la retta (y = mx + q).
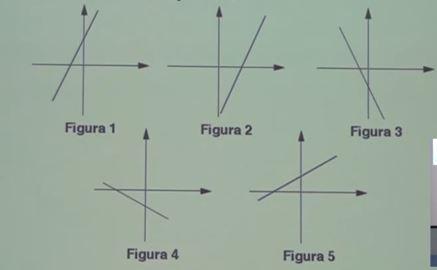
Fissato nel piano un sistema di assi cartesiani ortogonali Oxy, quale tra le seguenti è la retta di equazione 4x - 2y + 1 = 0?
Anche questo argomento in passato è comparso con una certa frequenza nei test di ammissione per l’università Bocconi.
Quello in questione è un semplice problema di geometria analitica, in quanto la retta è la funzione più semplice che possiamo studiare in 2D.
Riscriviamo la retta in forma canonica, portando il 2y al secondo membro: 4x + 1 = 2y, quindi abbiamo, dividendo tutto per 2:
y = 2x + ½
Il coefficiente angolare (coefficiente davanti alla x) è uguale a 2. Ricordandoci che il coefficiente angolare di una retta ne definisce la pendenza, possiamo rapidamente escludere le figure 3 e 4, che presentano rette con pendenza negativa (tra il secondo e il quarto quadrante).
L’inclinazione della retta 5 è minore di 1, in quanto la retta con inclinazione 1 è la bisettrice del primo e terzo quadrante, a 45 gradi con l’orizzontale. Escludiamo quindi anche questa retta.
Rimangono le figure 1 e 2 in cui le rette sembrano avere coefficiente angolare 2.
Notiamo a questo punto dalla nostra equazione in forma canonica, che l’intersezione con l’asse verticale y dovrebbe essere nel punto y = ½ (ponendo x =0), cioè sopra l’asse x. Tra le due opzioni rimaste, questo si verifica solo in figura 1, che è quindi necessariamente la nostra soluzione.
Accedi a tutti gli appunti
Tutor AI: studia meglio e in meno tempo
