Cominciamo a pubblicare le soluzioni 
Quesito n.1
[math] \lim_{ h\to 0} \frac{5\left(\frac{1}{2}+h\right)^4-5\left(\frac{1}{2}\right)^4}{h}
[/math]
[/math]
è il limite del rapporto incrementale (derivata) della funzione
[math] 5x^4 [/math]
calcolata nel punto
[math]x=\frac{1}{2} [/math]
[math] \lim_{ h\to 0} \frac{5\left(\frac{1}{16}+\frac{4}{8}h+\frac{6}{4}h^2+\frac{4}{2}h^3+h^4
\right)-\frac{5}{16}}{h}=\\
\lim_{h\to0}\frac{\left(\frac{5}{16}+\frac{5}{2}h+\frac{15}{2}h^2+10h^3+5h^4-\frac{5}{16}
\right)}{h} \\ \lim_{ h\to 0} \left(
\frac{5}{2}+\frac{15}{2}h+10h^2+5h^3\right)=\frac{5}{2}[/math]
\right)-\frac{5}{16}}{h}=\\
\lim_{h\to0}\frac{\left(\frac{5}{16}+\frac{5}{2}h+\frac{15}{2}h^2+10h^3+5h^4-\frac{5}{16}
\right)}{h} \\ \lim_{ h\to 0} \left(
\frac{5}{2}+\frac{15}{2}h+10h^2+5h^3\right)=\frac{5}{2}[/math]
oppure: sapendo che
[math] \lim_{ x\to 0} \left(
\frac{\left(1+x\right)^\alpha-1}{x}\right)=\alpha[/math]
\frac{\left(1+x\right)^\alpha-1}{x}\right)=\alpha[/math]
[math]
\lim_{h\to 0}\frac{5\left(\frac{1+2h}{2}\right)^4-5\left(\frac{1}{2}\right)^4}{h}=\lim_{h\to 0}\frac{5\left(\frac{1}{2}\right)^4\left(1+2h\right)^
4-5\left(\frac{1}{2}\right)^4} { h }=\\ \lim_{ h\to 0} \left(
\frac{5}{16}\frac{\left(1+2h\right)^4-1}{2h}2\right) \\
= \frac{10}{16}\lim_{ h\to 0} \left( \frac{\left(1+2h\right)^4-1}{2h}\right) [/math]
\lim_{h\to 0}\frac{5\left(\frac{1+2h}{2}\right)^4-5\left(\frac{1}{2}\right)^4}{h}=\lim_{h\to 0}\frac{5\left(\frac{1}{2}\right)^4\left(1+2h\right)^
4-5\left(\frac{1}{2}\right)^4} { h }=\\ \lim_{ h\to 0} \left(
\frac{5}{16}\frac{\left(1+2h\right)^4-1}{2h}2\right) \\
= \frac{10}{16}\lim_{ h\to 0} \left( \frac{\left(1+2h\right)^4-1}{2h}\right) [/math]
e siccome per
[math] h\rightarrow 0, 2h\rightarrow 0[/math]
allora
[math] \frac{5}{8}
\lim_{ h\to 0}
\frac{\left(1+2h\right)^4-1}{2h}=\frac{5}{8}4=\frac{5}{2}[/math]
\lim_{ h\to 0}
\frac{\left(1+2h\right)^4-1}{2h}=\frac{5}{8}4=\frac{5}{2}[/math]
[newpage]
Quesito n.2
sia
[math] f:\ \mathbb{R}\rightarrow \mathbb{R} [/math]
\\
1) se
[math] \lim_{ h\to 0} f\left(x\right)=\infty, a\in\mathbb{R}[/math]
allora
[math]x=a[/math]
si dice asintoto verticale\\
2) se
[math]\lim_{ h\to \pm\infty} f\left(x\right)=l,\;l\not= \infty \Rightarrow y=l[/math]
si dice asintoto orizzontale\\
3) se
[math]\lim_{ h\to \pm\infty} f\left(x\right)=\infty[/math]
e si ha\\
a)
[math]\lim_{ h\to \pm\infty}\frac{f\left(x\right)}{x}=m,\;m\not= 0,\;m\not= \infty[/math]
\\
b)
[math]\lim_{ h\to \pm\infty} \left(f\left(x\right)-mx\right)=q,\;q\not=\infty[/math]
\\
[math]\Rightarrow y=mx+q[/math]
si dice asintoto obliquo\\
ESEMPIO:
[math]f\left(x\right)=\frac{x^2}{x^2+2x-3}=\frac{x^2}{\left(x+3\right)\left(x-1\right)}[/math]
\\
D:
[math]x^2+2x-3\not= 0 \Rightarrow \left(x+3\right)\left(x-1\right)\not= 0 \Rightarrow x\not= -3,\; x\not= 1 [/math]
\\
[math] \lim_{x \to -3^-}f\left(x\right)=\frac{q}{\left(0^-\right)\left(-4\right)}=\frac{q}{0^+}=+\infty[/math]
\\
[math] \lim_{x \to -3^+}f\left(x\right)\frac{q}{\left(0^+1\right)\left(-4\right)}=\frac{q}{0^-}=-\infty[/math]
\\
analogamente sarà\\
[math] \lim_{x \to 1^- } \left(\frac{1}{4\left(0^-\right)}\right)=-\infty [/math]
\\
[math] \lim_{x \to 1^+ }\left(\frac{1}{\left(4\right)\left(0^+\right)}\right)=\frac{1}{0^+}=+\infty[/math]
\\
inoltre
[math]\lim_{x \to +\infty}\frac{x^2}{x^2+2x-3}=\frac{x^2}{x^2\left(1+\frac{2}{x}-\frac{3}{x^2}\right)}=1[/math]
[newpage]
Quesito n.3
[math] S(t) = 20 (2e^{-\frac{t}{2}} + t - 2)[/math]
Sapendo che:
[math] V = \frac{\delta s}{\delta t} = S'(t)[/math]
e che:
[math]a(t) = \frac{\delta v}{\delta t} = \frac{S'(t)}{\delta t} = S''(t)[/math]
[math]S'(t) = 20 (1 - e^{-\frac{t}{2}}) = -20 (e^{-\frac{t}{2}} - 1)[/math]
La derivata della somma è uguale alla somma delle derivate
[math] D [t] = 1 \to D [2e^{-\frac{t}{2}}] = \not{2}e^{-{\frac{t}{2}}} \cdot - \frac{1}{\not{2}} = -e^{-{\frac{t}{2}}[/math]
[math]D[-2] = 0[/math]
[math]S''(t) = -20 (e^{-{\frac{t}{2}}} \cdot - \frac{1}{2}) = -20(-\frac{e^{-\frac{t}{2}}}{2})[/math]
[math] \frac{20e^{-\frac{t}{2}}}{2} = 10e^{-{\frac{t}{2}}[/math]
e quindi:
[math]S''(4) = 10^{-\frac{4}{2}} = 10^ {-2} = \frac{1}{10^2} = \frac{1}{100}[/math]
[newpage]
Quesito n.4
Apotema = 1 m
r = raggio di base
[math]r \geq 0[/math]
[math]h = \sqrt{1 - r^2}[/math]
[math]V = \frac{1}{3} \pi \ r^2 h \to V(r) = \frac{\pi}{3} \ r^2 \sqrt{1 - r^2} = [/math]
[math]\frac{\pi}{3} (r^2 \sqrt{1 - r^2})[/math]
[math]V'(r) = \frac{\pi}{3} \ ( 2r \sqrt{1 r^2} + r^2 \cdot \frac{1}{2\sqrt{1-r^2}} \cdot - 2r \)[/math]
[math]\frac{\pi}{3} (2r\sqrt{1 - r^2} - 2r \frac{r^2}{2\sqrt{1-r^2}}) =[/math]
[math]2r \frac{\pi}{3} (\sqrt{1 - r^2} - \frac{r^2}{2\sqrt{1 - r^2}})=[/math]
[math]2r \frac{\pi}{3} \( \frac{(1-r^2) - r^2}{2\sqrt{1- r^2}} \) =[/math]
[math]2r \frac{\pi}{3} \( \frac{1 - 2r^2}{2\sqrt{1 - r^2}} \) =[/math]
[math]V' (r) > 0 \to 2r \frac{\pi}{3} (\frac{1 - 2r^2}{2\sqrt{1 - r^2}}) > 0[/math]
[math]2r \frac{\pi}{3} > 0 \ \forall r \in C.E.[/math]
[math]2 \sqrt{1 - r^2} > 0 \ \forall r \in C.E.[/math]
[math]1 - 2r^2 > 0 \to 2r^2 > 1 = [/math]
[math]r^2 > \frac{1}{2} \to -\frac{\sqrt2}{2} > r > \frac{\sqrt2}{2} = 0 > r > \frac{\sqrt2}{2}[/math]
Volume massimo per:
[math]r = \frac{\sqrt2}{2} \to h = \sqrt{1 - \frac{1}{2} = \sqrt{\frac{1}{2} = \frac{\sqrt2}{2}[/math]
[math]V = \frac{\pi}{3} r^2h = \frac{1}{2} \frac{\pi}{3} \frac{\sqrt2}{2} = \frac{1}{12} \sqrt2 \pi[/math]
[newpage]
Quesito n.5
[newpage]
Quesito n.6
Quesito 6 - scientifico tradizionale
[math] D (5\sin x \cos x) = -5 \sin^2 x + 5 \cos^2 x[/math]
[math] D(\cos^2 x) = -2 \cos x \sin x[/math]
[math] D(-sin^2 x) = -2 \sin x \cos x[/math]
[math] D(-\frac{5}{2} \sin 2x) = - \frac{5}{2} \cos 2x - 2 = -5 \cos 2x[/math]
[math] D(-\cos 2x) = + \sin 2x \cdot 2 = 2 \sin 2x[/math]
[math] f'(x) = - 5 \sin^2 x + 5 \cos^2 x - 2 \sin x \cos x -2 \sin x \cos x - 5 \cos 2x + 2 \sin 2x = [/math]
[math]5 cos 2x - 2 \sin 2x - 5 cos 2x + \sin 2x = 0 [/math]
[newpage]
Quesito n.7
Si consideri la base del tetraedro.
Esso è un triangolo equilatero di lato e per ipotesi.
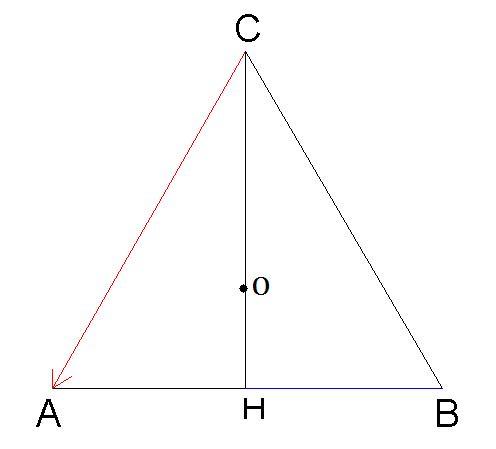
Altezza :
[math] \frac{l\sqrt3}{2}[/math]
Calcoliamo AO sapendo che OH =
[math]\frac{2}{3}h = \frac{l}{3}\sqrt3[/math]
L'altezza del tetraedro sarà:
[math]\sqrt{l^2 - \frac{l^2}{3}} = \sqrt{\frac{2}{3}l^2} = l \sqrt{2}{3}[/math]
L'angolo tra l e h è l'angolo del triangolo rettangolo compreso tra h (cateto) e l (ipotenusa).
Detto x l'angolo:
[math]\cos x = \frac{l}{l\sqrt{\frac{3}{2}}} = \frac{2}{3}[/math]
da cui x =
[math] arccos \sqrt{2}{3} \approx 35^{\circ}26'[/math]
[newpage]
Quesito n.8
Valore medio (Teorema di Lagrange)
[math] \frac{f(a) - f(b)}{b - a}[/math]
[math]\frac{f(1) - f(e)}{e-1} = \frac{1 - \frac{1}{e}}{e-1} = \frac{\frac{\not{e-1}}{e}}{\not{e-1}} = {\frac{1}{e}[/math]
Valore medio integrale
[math]\frac{1}{b-a} \int_{a}^{b} f(x)dx =[/math]
[math]\frac{1}{e-1} \int_{1}^{e} \frac{1}{x}dx =[/math]
[math]\frac{1}{e-1} [\log(x)\]^e_1 = \frac{1}{e-1} (\log e - \log 1) =[/math]
[math]\frac{1}{e-1} (1 -0) = \frac{1}{e-1}[/math]
[newpage]
Quesito n.9
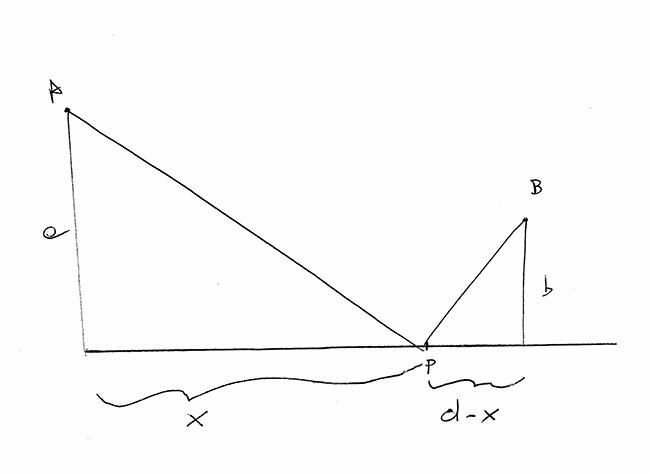
[math]d\left(x\right)=AP+PB[/math]
supponiamo
[math]b>a[/math]
[math]AP=\sqrt{a^2+x^2}[/math]
\\
[math]PB=\sqrt{b^2+\left(d-x\right)^2}[/math]
[math]d\left(x\right)=\sqrt{a^2+x^2}+\sqrt{b^2+\left(d-x\right)^2}[/math]
\\
[math]d'\left(x\right)=\frac{x}{\sqrt{a^2+x^2}}-\frac{d-x}{\sqrt{b^2+\left(d-x\right)^2}}=0 \Leftrightarrow
x\sqrt{b^2+\left(d-x\right)^2}=[/math]
x\sqrt{b^2+\left(d-x\right)^2}=[/math]
[math]\left(d-x\right)\sqrt{a^2+x^2}[/math]
\\
[math]x^2\left[b^2+\left(d-x\right)\right]=\left(d-x\right)^2\left(a^2+x^2\right)[/math]
\\
[math]x^2b^2+x^2\left(d-x\right)^2=a^2\left(d-x\right)^2+x^2\left(d-x\right)^2 [/math]
\\
[math]x^2b^2-a^2\left(d^2-2dx+x^2\right)=0[/math]
\\
[math]\left(a^2-b^2\right)x^2-2a^2dx+a^2d^2=0 [/math]
\\
[math]x_{1,2}=\frac{2a^2d\pm\sqrt{4a^4d^2-4a^2d^2\left(x^2-b^2\right)}}{2\left(a^2-b^2\right)}=[/math]
\\
[math]\frac{2a^2d\pm\sqrt{4a^2b^2d^2}}{2\left(a^2-b^2\right)}=\frac{2a^2d\pm2abd}{2\left(aì2-b^2\right)}= [/math]
\\
[math]\frac{2ad\left(a\pm b\right)}{2\left(a^2-b^2\right)}[/math]
\\
[math]\Rightarrow x_1=\frac{ad}{a+b},\; x_2=\frac{ad}{a-d}[/math]
\\
[math]d-x_1=\frac{db}{a+b}\;\;\;\;d-x_2=-\frac{bd}{a-b}>0\Rightarrow assurdo[/math]
\\
[math]x_2 e d-x_1 soluzione \Rightarrow\frac{x_1}{d-x_1}=\frac{a}{b}[/math]
[newpage]
Quesito n.10
[math]x^2 + 1 \geq 1 \ \forall x \in \mathbb{R}[/math]
Osserviamo che:
A)
[math]\sin (x^2 + 1) \in [-1; 1][/math]
B)
[math]\cos (x^2 + 1) \in [-1; 1][/math]
C)
[math]ln (x^2 + 1) \in [ 0 ; + \inft] [/math]
D) Come sopra.
Dal momento che:
[math][-1, 1] \leq (- \frac{\pi}{2} , \frac{\pi}{2})[/math]
e il coseno ristretto a tale intervallo è sempre
[math]\geq 0[/math]
, segna che
[math]\cos \( \sin (x^2 + 1 ) \) > 0 \ \forall x \in \mathbb{R}[/math]
Le altre non sono verificate poiché il seno di valori negativi è negativo (caso B) e
per la periodicità di sen e cos su
[math][o, + \inft][/math]
(casi C e D)
Accedi a tutti gli appunti
Tutor AI: studia meglio e in meno tempo
