[math]T[/math]
il periodo della funzione [math]g[/math]
: allora si ha [math]g(x+T)=g(x)[/math]
per ogni [math]x\in\mathbb{R}[/math]
. Dunque
[math]\sin\left(\frac{3\pi}{2} x+\frac{3\pi}{2} T\right)=\sin\left(\frac{3\pi}{2} x\right),[/math]
e posto
[math]y=\frac{3\pi}{2} x[/math]
, [math]P=\frac{3\pi}{2} T[/math]
[math]\sin(y+P)=\sin(y)\ \Rightarrow\ P=2\pi\ \Rightarrow\ T=\frac{4}{3}.[/math]
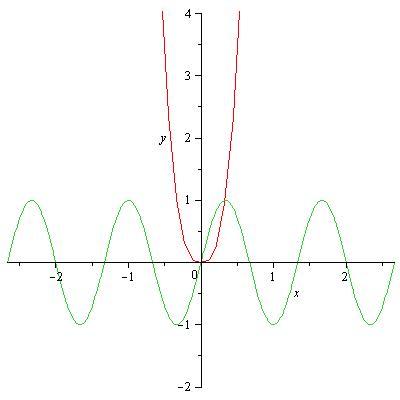
Studiamo le due funzioni:
[math]Dom(f)=Dom(g)=\mathbb{R}.[/math]
Inoltre
[math]lim_{x\to\pm\infty} f(x)=+\infty,\qquad m=\lim_{x\to\pm\infty} \frac{f(x)}{x}=\pm\infty,[/math]
e quindi non ci sono asintoti obliqui.
Scrivendo poi
[math]f(x)=\left\{\begin{array}{lcl}
27 x^3 & & x\geq 0\\ -27 x^3 & & x \end{array}\right.[/math]
27 x^3 & & x\geq 0\\ -27 x^3 & & x \end{array}\right.[/math]
si ha
[math]f'(x)=\left\{\begin{array}{lcl}
81 x^2 & & x\geq 0\\ -81 x^2 & & x \end{array}\right.[/math]
81 x^2 & & x\geq 0\\ -81 x^2 & & x \end{array}\right.[/math]
e quindi
[math]f'(x)\ge 0[/math]
se e solo se [math]x\ge 0[/math]
, per cui la funzione cresce su [math](0,+\infty)[/math]
, decresce su [math](-\infty,0)[/math]
ed ha un minimo assoluto in [math]O(0,0)[/math]
dove presenta un punto angoloso. Inoltre
[math]f''(x)=\left\{\begin{array}{lcl}
162 x & & x\geq 0\\ -162 x & & x \end{array}\right.[/math]
162 x & & x\geq 0\\ -162 x & & x \end{array}\right.[/math]
per cui
[math]f''(x)\ge 0[/math]
per ogni [math]x\in\mathbb{R}[/math]
.Per la funzione
[math]g[/math]
, osserviamo che[math]g'(x)=\frac{3\pi}{2}\cos\left(\frac{3\pi}{2} x\right)\geq 0,[/math]
se e solo se
[math]0\leq \frac{3\pi}{2} x\leq \frac{\pi}{2},\qquad \frac{3\pi}{2}\le\frac{3\pi}{2} x\leq 2\pi,[/math]
e quindi
[math]0\leq x\leq \frac{1}{3},\qquad 1\leq x\leq \frac{4}{3},[/math]
pertanto i punti
[math]A(1/3,1)[/math]
e [math]B(1,-1)[/math]
sono, rispettivamente, massimo e minimo assoluto.
Si ha poi
[math]g''(x)=-\frac{9\pi^2}{4}\sin\left(\frac{3\pi}{2} x\right)\geq 0,[/math]
se e solo se
[math]\pi\leq\frac{3\pi}{2} x\leq 2\pi\ \Rightarrow\ \frac{2}{3}\leq x\leq \frac{4}{3},[/math]
e quindi la funzione presenta flessi nei punti
[math]O(0,0),\ C(2/3,0),\ D(4/3,0)[/math]
.Il grafico delle funzione è riportato in figura seguente.
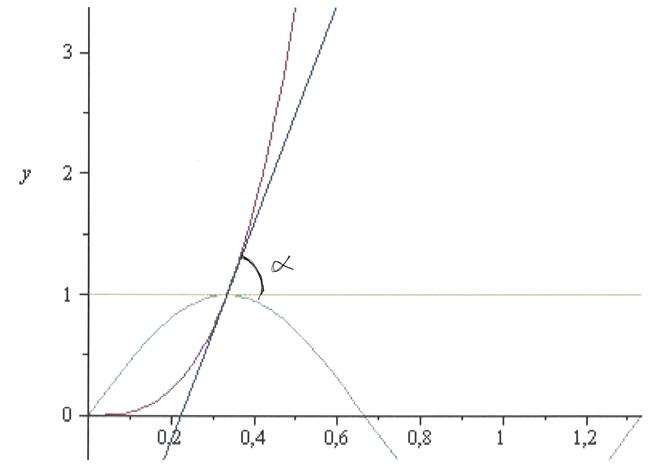
2. Se
[math]P(x_0,F(x_0))[/math]
è il punto dove determinare la tangente alla curva [math]y=F(x)[/math]
allora usiamo la formula[math]y-F(x_0)=F'(x_0)(x-x_0).[/math]
Abbiamo allora
[math]y-f(1/3)=f'(1/3)(x-1/3)\ \Rightarrow\ y-1=81(1/9)(x-1/3)\ \Rightarrow\ y=9x-2,[/math]
[math]y-g(1/3)=g'(1/3)(x-1/3)\ \Rightarrow\ y-1=(3\pi/2)(\cos(\pi/2))(x-1/3)\ \Rightarrow\ y=1.[/math]
Le due rette sono allora
[math]y=9x-2,\qquad y=1,[/math]
e l'angolo da esse formato, essendo la seconda parallela all'asse x, coincide con l'angolo della prima: valendo la condizione
[math]m=\tan\alpha[/math]
, dove [math]m[/math]
è il coefficiente angolare mentre [math]\alpha[/math]
l'angolo formato dalla retta con l'asse x, abbiamo[math]9=\tan\alpha\ \Rightarrow\ \alpha=\arctan 9=88,66^\circ=88^\circ\ 34'.[/math]
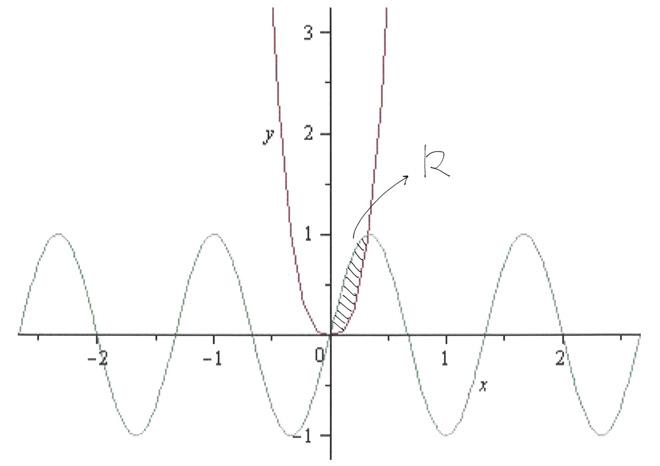
3. Calcoliamo l'area usando l'integrazione: dal momento che il punto di intersezione delle curva è
[math]A(1/3,1)[/math]
allora[math]S=\int_0^{1/3}[g(x)-f(x)]\ dx=\int_0^{1/3}\left[\sin\left(\frac{3\pi}{2} x\right)-27 x^3\right]\ dx=[/math]
[math]=\left[-\frac{2}{3\pi}\cos\left(\frac{3\pi}{2} x\right)-\frac{27}{4} x^4\right]_0^{1/3}=[/math]
[math]=-\frac{2}{3\pi}\cos\left(\frac{\pi}{2}\right)-\frac{27}{4}\cdot\frac{1}{81}+\frac{2}{3\pi}\cos 0+0=[/math]
[math]=-\frac{1}{12}+\frac{2}{3\pi}=\frac{8-\pi}{3\pi}.[/math]
4. Se
[math]y=f(x),\ x=F(y)[/math]
sono una funzione inversa dell'altra, in modo che [math](x_0,y_0)[/math]
è il punto per cui [math]y_0=f(x_0),\ x_0=F(y_0)[/math]
, allora i volumi dei solidi di rotazione, rispettivamente rispetto all'asse x e all'asse y si trovano usando gli integrali
[math]V_x=\pi\int_0^{x_0} [f(x)]^2\ dx,\qquad V_y=\pi\int_0^{y_0}[F(y)]^2\ dy.[/math]
Pertanto abbiamo
[math]V_x=\pi\int_0^{1/3}\left\{[g(x)]^2-[f(x)]^2\right\}\ dx,[/math]
[math]V_y=\pi\int_0^1\left\{[F(y)]^2-[G(y)]^2\right\}\ dy,[/math]
dove
[math]F,G[/math]
sono, rispettivamente, le funzioni inverse di [math]f,g[/math]
.
Accedi a tutti gli appunti
Tutor AI: studia meglio e in meno tempo
