Matematica (PNI)

Genius

6 min. di lettura

Vota

Quesito n.1

[math]\lim_{x \to 0^+} \frac{2^{3x} - 3^{4x}}{x} =[/math]

[math]\lim_{x \to 0^+} \frac{2^{3x} - 1 + 1 - 3^{4x}}{x} = [/math]

[math]\lim_{x \to 0^+} [\frac{(2^3)^x - 1}{x} - \frac{(3^4)^x - 1}{x}] =[/math]

[math]ln \ 2^3 - ln \ 3^4 = 3 ln \ 2 - 4 ln \ 3[/math]
dove si è usato il limite notevole:

[math]\lim_{x \to 0^+} \frac{a^x - 1}{x} = ln \ a \to a > 0[/math]
[newpage]
Quesito n.2
Sia d=23.25mm il diametro. Il centro della moneta, affinché essa cada nell'esagono, deve trovarsi ad una distanza,
[math]s=\frac{d}{2}[/math]
dal bordo.
Se l è il lato dell'esagono. Per determinare il lato dell'esagono interno come in figura

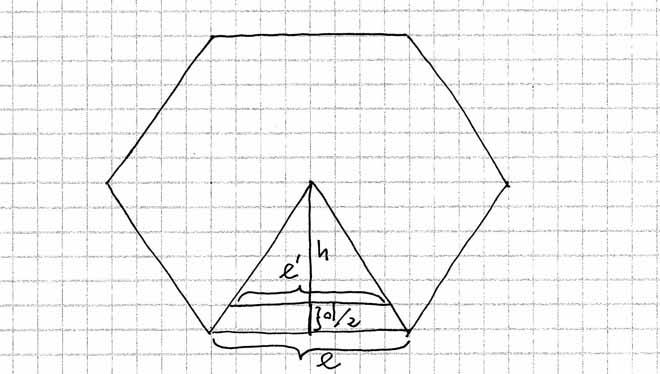
si può sfruttare il fatto che
[math]\frac{l'}{l}=\frac{h}{h+\frac{d}{2}}[/math]
\\
Poiché
[math]h=\frac{\sqrt{3}}{2}l'\Rightarrow[/math]
[math]\frac{l'}{l}=\frac{\frac{\sqrt3}{2}l'}{\frac{\sqrt{3}}{2}l'+\frac{d}{2}}[/math]
\\
[math]\Rightarrow\frac{\sqrt{3}}{2}l'+\frac{d}{2}=\frac{\sqrt{3}}{2}l\Rightarrow l'=l-\frac{d}{\sqrt{3}}[/math]
\\
la probabilità è pari a rapporto delle aree, per cui:
[math]A=6\cdot \frac{1}{2}l\left(h+\frac{d}{2}\right)[/math]
\\
[math]A'=6\cdot \frac{1}{2}l'\left(h\right)=3h\left(l-\frac{d}{\sqrt{3}}\right)[/math]
\\
[math]P=\frac{h\left(l-\frac{d}{\sqrt{3}}\right)}{l\left(h+\frac{d}{2}\right)} =[/math]
\\
[math]\frac{\left(\frac{\sqrt{3}}{2}l-\frac{d}{2}\right)\left(l-\frac{d}{\sqrt{3}}\right)}{l\left(\frac{\sqrt{3}}{2}l\right)
}=[/math]
\\
[math]\frac{\frac{\sqrt{3}}{2}l^2-\frac{d}{2}l-\frac{d}{2}l-\frac{d}{2\sqrt{3}}}{l^2\frac{\sqrt{3}}{2}}=[/math]
\\
[math]\frac{\frac{3}{2}l^2-dl-\frac{d}{2\sqrt{3}}}{l^2\cdot\frac{\sqrt{3}}{2}}\simeq0.73[/math]
[newpage]
Quesito n.3
[newpage]
Quesito n.4
Per far vedere questo fatto, procediamo nel
modo seguente. Costruiamo la seguente tabella:
[math]\begin{array}{ccccccc}
1/1 & 1/2 & 1/3 & 1/4 & 1/5 & 1/6 & .....\\
2/1 & 2/2 & 2/3 & 2/4 & 2/5 & 2/6 & .....\\
3/1 & 3/2 & 3/3 & 3/4 & 3/5 & 3/6 & .....\\
4/1 & 4/2 & 4/3 & 4/4 & 4/5 & 4/6 & .....\\
5/1 & 5/2 & 5/3 & 5/4 & 5/5 & 5/6 & .....\\
6/1 & 6/2 & 6/3 & 6/4 & 6/5 & 6/6 & .....\\
7/1 & 7/2 & 7/3 & 7/4 & 7/5 & 7/6 & .....
\end{array}[/math]
Possiamo ordinare i numeri nel modo seguente, eliminando le copie:
[math]1,\ 1/2,\ 2,\ 3,\ 1/3,\ 1/4,\ 2/3,\ 3/2,\ 4,\ 5,\ 1/5,[/math]
[math]1/6,\ 2/5,\ 3/4,\ 4/3,\ 5/2,\ 6,\ 7,\ 5/3,\ 3/5, \ldots[/math]
A questo punto, associando ogni numero positivo con un numero
dispari e il suo corrispondente negativo con uno pari otteniamo
una relazione che collega ogni numero razionale ad un numero
naturale.
[newpage]
Quesito n.5
[newpage]
Quesito n.6
[math]f'(x) = 3x^2 + a[/math]

[math]f''(x) = 6^2 = 0 \Leftrightarrow \ x = 0[/math]
(flesso)
L'equazione generale di una simmetria rispetta ad un punto (Xo, Yo) è:

[math]\{ x' = 2x_0 - x \\ y' = 2y_0 - y[/math]
Da cui:

[math]\{x = 2x_0 - x' \\ y = 2y_0 - y'[/math]
Sostituendo
[math] x_0 e 0_1, \ y_0 = f(x_0) = b[/math]
allora

[math]2b - y' = (-x')^3 + a (-x') + b \to[/math]

[math]-y' = -x'^3 - a \ x' + b - 2b[/math]

[math]y' = - x'^3 + a \ x' + b[/math]
Le funzioni risultano uguali, per cui c'è simmetria.
[newpage]
Quesito n.7
Si consideri la base del tetraedro. Esso è un triangolo equilatero di lato e per ipotesi.

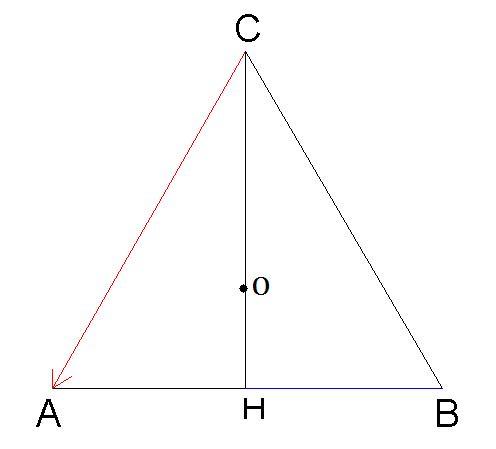
Altezza :
[math] \frac{l\sqrt3}{2}[/math]

Calcoliamo AO sapendo che OH =
[math]\frac{2}{3}h = \frac{l}{3}\sqrt3[/math]
L'altezza del tetraedro sarà:

[math]\sqrt{l^2 - \frac{l^2}{3}} = \sqrt{\frac{2}{3}l^2} = l \sqrt{2}{3}[/math]
L'angolo tra l e h è l'angolo del triangolo rettangolo compreso tra h (cateto) e l (ipotenusa).
Detto x l'angolo:

[math]\cos x = \frac{l}{l\sqrt{\frac{3}{2}}} = \frac{2}{3}[/math]
da cui x =
[math] arccos \sqrt{2}{3} \approx 35^{\circ}26'[/math]
[newpage]
Quesito n.8
[newpage]
Quesito n.9

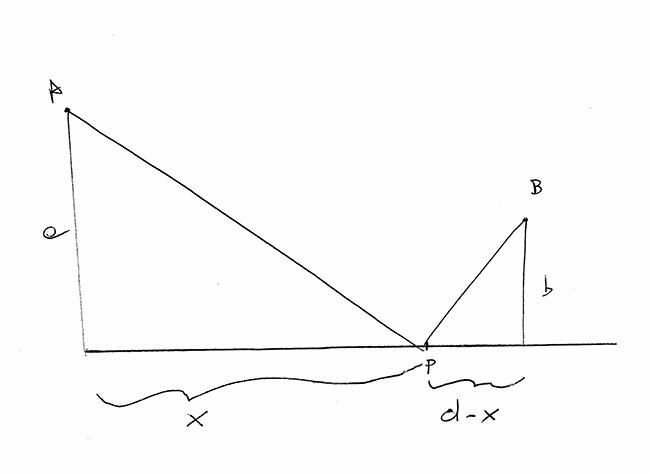
[math]d\left(x\right)=AP+PB[/math]
supponiamo
[math]b>a[/math]
[math]AP=\sqrt{a^2+x^2}[/math]
\\
[math]PB=\sqrt{b^2+\left(d-x\right)^2}[/math]

[math]d\left(x\right)=\sqrt{a^2+x^2}+\sqrt{b^2+\left(d-x\right)^2}[/math]
\\
[math]d'\left(x\right)=\frac{x}{\sqrt{a^2+x^2}}-\frac{d-x}{\sqrt{b^2+\left(d-x\right)^2}}=0 \Leftrightarrow
x\sqrt{b^2+\left(d-x\right)^2}=[/math]
[math]\left(d-x\right)\sqrt{a^2+x^2}[/math]
\\
[math]x^2\left[b^2+\left(d-x\right)\right]=\left(d-x\right)^2\left(a^2+x^2\right)[/math]
\\
[math]x^2b^2+x^2\left(d-x\right)^2=a^2\left(d-x\right)^2+x^2\left(d-x\right)^2 [/math]
\\
[math]x^2b^2-a^2\left(d^2-2dx+x^2\right)=0[/math]
\\
[math]\left(a^2-b^2\right)x^2-2a^2dx+a^2d^2=0 [/math]
\\
[math]x_{1,2}=\frac{2a^2d\pm\sqrt{4a^4d^2-4a^2d^2\left(x^2-b^2\right)}}{2\left(a^2-b^2\right)}=[/math]
\\
[math]\frac{2a^2d\pm\sqrt{4a^2b^2d^2}}{2\left(a^2-b^2\right)}=\frac{2a^2d\pm2abd}{2\left(aì2-b^2\right)}= [/math]
\\
[math]\frac{2ad\left(a\pm b\right)}{2\left(a^2-b^2\right)}[/math]
\\
[math]\Rightarrow x_1=\frac{ad}{a+b},\; x_2=\frac{ad}{a-d}[/math]
\\
[math]d-x_1=\frac{db}{a+b}\;\;\;\;d-x_2=-\frac{bd}{a-b}>0\Rightarrow assurdo[/math]
\\
[math]x_2 e d-x_1 soluzione \Rightarrow\frac{x_1}{d-x_1}=\frac{a}{b}[/math]
[newpage]
Quesito n.10
[newpage]

Matematica (PNI) - Quesiti

Soluzione dei quesiti di matematica del liceo scientifico, PNI, assegnata alla maturità 2012

Recensioni

Domande e risposte

I migliori insegnanti di Ripetizioni

Giovanni C.

Salvatore F.

Appunti correlati

Matematica (PNI) - Soluzione Completa

Matematica (PNI) - Soluzione Problema 1

Matematica (PNI) - Soluzione Problema 2

Matematica (corso ordinario) - Quesiti

Recensioni

Domande e risposte

I migliori insegnanti di Ripetizioni

Giovanni C.

Salvatore F.