vuoi
o PayPal
tutte le volte che vuoi

State cercando la pagina della soluzione della seconda prova matematica per il liceo scientifico? Qui potrete confrontare la prova svolta dai nostri preparatissimi tutor con le vostre risposte e levarvi ogni dubbio. Preparatevi al confronto, quindi, e ricordate che noi di Skuola.net renderemo disponibile la soluzione della seconda prova maturità liceo scientifico solo a partire dall’orario consentito per legge. E se con un occhio state già guardando all’orale, vi ricordiamo noi tutto ciò che serve sapere sulla commissione!
Vi invitiamo quindi caldamente a non consultare questa pagina prima di aver consegnato il compito e di essere usciti dall’aula d’esame. Farsi invalidare la seconda prova così sarebbe davvero sciocco!
Siete a metà strada, il diploma si avvicina sempre più, quindi mettetecela tutta nello svolgere i problemi e i vari quesiti di questa seconda prova. La concentrazione è tutto: se rimarrete con la testa sul compito e utilizzerete tutte le conoscenze acquisite nel corso dell’anno non potrà che andare bene.
Siete pronti a confrontarvi coi nostri tutor? Qui di seguito pubblicheremo le soluzioni della prova di matematica!
Soluzione problema 1 matematica
Qui troverete la soluzione del primo problema di matematica della seconda prova di matematica del liceo scientifico. La pagina è in aggiornamento!




Soluzione problema 2 matematica
Punto 1
Dato
Cerchiamo ora le equazioni delle rette tangenti
Per i coefficienti angolari calcolo la derivata prima:
Per l'equazione completa utilizziamo la formula della retta passante per un punto assegnato. Dunque per
Per
Per trovare il punto di intersezione
\begin{cases}
y=kx+9\\
y=(k-3)x+11\\
\end{cases}
\begin{cases}
y=kx+9\\
kx+9(k-3)x+11\\
\end{cases}
[/math]
\begin{cases}
y=kx+9\\
-3x+11=9\\
\end{cases}
\begin{cases}
y=\frac{2}{3}+9\\
x=\frac{2}{3}\\
\end{cases}
[/math]
Dunque
Punto 2
L'ordinata del punto
Basta allora imporre alla funzione la condizione richiesta:
Poiché
Sia dunque
Dominio: la funzione è polinomiale intera, perciò definita su tutto
Derivata prima:
I punti stazionari sono:
Le corrispondenti ordinate sono:
Studiamo il segno della derivata prima:
quindi, essendo un polinomio di grado 2, con coefficiente del termine quadratico negativo, è rappresentabile da una parabola con concavità rivolta verso il basso. Si può concludere che assuma valori nulli o positivi per
Studio degli asintoti
Essendo definita su tutto l'asse reale, i limiti vanno studiati solo all'infinito. Calcoliamo:
Derivata seconda
Cerchiamo eventuali punti di flesso calcolando la derivata seconda, e ponendola uguale a 0:
Quindi troviamo un punto di flesso
Grafico approssimativo
_____________________________________________
Punto 3
I vertici del triangolo richiesto sono:
L'intersezione tra la retta
L'intersezione tra la retta
L'intersezione tra le rette
Ricordiamo che la probabilità di scegliere un punto
Calcoliamo l'area del triangolo:
Invece l'area della sezione voluta può essere ottenuta come differenza tra la regione totale, e:
Area del triangolo
Area sottesa dal grafico della funzione
Per trovare il punto
- Utilizzando la calcolatrice grafica, si trova
- Sfruttando il metodo di bisezione, si parte con
Fermando l'iterazione a questo valore di
Per il calcolo dell'area, si procede con l'integrale definito nell'opportuno intervallo.
I=\int_0^c(-x^3+x+9)\,dx=\left[-\frac{x^4}{4}+\frac{x^2}{2}+9x\right]_0^c
[/math]
Nel caso di
Nel caso di
Quindi otteniamo la probabilità, nei due casi:
Punto 4
Consideriamo il fascio di rette passanti per l'origine, che ha equazione:
Un polinomio generico di grado
Formalmente, la sua derivata è:
che, ovviamente, è un polinomio di grado
Sia
Osserviamo che, essendo
Se ora imponiamo il passaggio della retta generica
\begin{split}
&y_N=-\frac{1}{P_n'(x_N)}x_N \\
&P_n(x_N)=-\frac{x_N}{P_n'(x_N)} \\
&P_n(x_N)P_n'(x_N)=-x_N \\
&P_n(x_N)P_n'(x_N)+x_N=0 \\
\end{split}
[/math]
Si tratta di un'equazione polinomiale di grado
_____________________________
___________________________
Quesito 1
Indichiamo l'altezza e il raggio del cono con
\frac{\pi R^2 H}{3}
[/math]
e il volume del cilindro è
\pi r^2 h.
[/math]
Poniamo
V(x)=\frac{\pi(R-x)^2xH}{R}=\frac{\pi H (x^3-2Rx^2+R^2x)}{R}.
[/math]
Per dimostrare quanto richiesto, calcoliamo il massimo della funzione
La derivata
V'(x)=\frac{\pi H (3x-R)(x-R)}{R},
[/math]
che si annulla in
f\left(\frac{R}{3}\right)=\frac{4}{9}\cdot\frac{\pi R^2 H}{3},
[/math]
che è uguale a
Quesito 2
La probabilità di ottenere ciascun valore si ricava dalla condizione assegnata:
\begin{split}
&p(1)=2p(2)=4p(3)=8p(4)\quad\text{per cui}\\
&p(1)=2p(2)\\
&p(2)=2p(3)\\
&p(3)=2p(4)\\
\end{split}
[/math]
e dal fatto che la somma delle probabilità deve dare 1. Quindi si ottiene:
\begin{split}
&p(1)+p(2)+p(3)+p(4)=1 \\
&\left(8+4+2+1)p(4)=15p(4)=1\right)\\
&p(4)=\frac{1}{15}
\end{split}
[/math]
La probabilità di ottenere due volte lo stesso valore è il prodotto della probabilità di singola uscita; ovviamente vanno sommate le probabilità relative a tutti i singoli valori possibili:
p^2(1)+p^2(2)+p^2(3)+p^2(4)=\frac{8^2+4^2+2^2+1^2}{15^2}=\frac{85}{15^2}=\frac{17}{45}
[/math]
______
___
______
Quesito 3
Chiamiamo
\begin{cases}
f(x_T)=g(x_T)\\
f'(x_T)=g'(x_T)
\end{cases}
[/math]
Dobbiamo quindi risolvere il sistema
\begin{cases}
-4x_T+k=x_T^3-4x_T^2+5\\
-4=3x_T^2-8x_T
\end{cases}
[/math]
La seconda equazione, che è un'equazione di secondo grado in
Quesito 4
Per valutare il primo limite notiamo che le funzioni trigonometriche possono essere maggiorate o minorate a seconda dell'esigenza. Essendo il loro valore compreso tra
0<\lim_{x\to\infty}\frac{3x-e^{\sin(x)}}{5+e^{-x}+\cos(x)}\geq\lim_{x\to\infty}\frac{3x-e^{-1}}{5+e^{-x}-1}=\frac{\infty-\frac{1}{e}}{5+0-1}=\infty
[/math]
Dunque il primo limite è
Per valutare il secondo limite è comodo dividere sia il numeratore sia il denominatore per
\lim_{x\to-\infty}\frac{3x-e^{\sin(x)}}{5+e^{-x}+\cos(x)}=\lim_{x\to-\infty}\frac{\frac{3x-e^{\sin(x)}}{e^{-x}}}{\frac{5+e^{-x}+\cos(x)}{e^{-x}}}
[/math]
Il numeratore può essere trattato in maniera analoga al limite precendete:
\lim_{x\to-\infty}\frac{3x-e}{e^{-x}}<\lim_{x\to-\infty}\frac{3x-e^{\sin(x)}}{e^{-x}}<0
[/math]
e dato che il primo limite va a zero per la gerarchia degli infiniti, il numeratore tende a zero in virtù del teorema dei carabinieri.
Il denominatore può essere scomposto in tre rapporti:
\lim_{x\to-\infty}\left[\frac{5}{e^{-x}}+\frac{e^{-x}}{e^{-x}}+\frac{\cos(x)}{e^{-x}}\right]
[/math]
Il primo limite è nullo, il secondo è
Infine, il limite del rapporto tra numeratore e denominatore tende a
Quesito 5
Indichiamo con x il raggio in metri della semicirconferenza. Un lato del rettangolo è quindi lungo 2x. Indichiamo con y la lunghezza in metri dell'altro lato. Il perimetro e l'area della figura, che è l'unione di un rettangolo e un semicerchio, in funzione di x e y sono rispettivamente
e
Ricordando che il perimetro è 2 metri, dall'uguaglianza
Usando quest'ultima relazione, esprimiamo in funzione di x l'area A(x) della figura
\begin{split}
&A(x)=2x\cdot \frac{2-(2+\pi)x}{2}+\frac{\pi x^2}{2} =\\
& \frac{-(4+\pi) x^2+4x}{2}
\end{split}
[/math]
La funzione A(x) è un polinomio di secondo grado in x e quindi il suo grafico è una parabola. Poiché il coefficiente del termine di secondo grado è negativo, il massimo di A(x) viene assunto nell'unico punto in cui si annulla la sua derivata, che è
Si annulla in
Le dimensioni dei lati del rettangolo sono quindi
______________________
Quesito 6
Un vettore perpendicolare al piano è
\begin{cases}
x=3s-4\\
y=-s\\
z=-2s+1
\end{cases} \quad s \in \mathbf{R}
[/math]
Il centro di
\begin{cases}
3s-4=t\\
-s=t\\
-2s+1=t
\end{cases}
[/math]
otteniamo
(x+1)^2+(y+1)^2+(z+1)^2=14
[/math]
Quesito 7
Calcoliamo l'integrale proposto in funzione di
\begin{split}
&\int_a^{a+1} (3x^2+3) dx = [x^3+3x]_{a}^{a+1}=\\
&(a+1)^3+3(a+1)-(a^3+3a)=3a^2+3a+4.
\end{split}
[/math]
Affinché l'integrale sia uguale a
3a^2+3a+4=10.
[/math]
Quest'ultima equazione, di secondo grado in
Quesito 8
Chiamiamo
La probabilità
p(10)=2\cdot \left(\frac{1}{2}\right)^{10} = \frac{1}{2^9}.
[/math]
Il gioco termina dopo
p(11)=2\cdot \left(\binom{11}{10} - \binom{10}{10}\right) \cdot \left(\frac{1}{2}\right)^{11} = \frac{5}{2^9}.
[/math]
Il gioco termina dopo
p(12)=2\cdot \left(\binom{12}{10} - \binom{11}{10}\right) \cdot \left(\frac{1}{2}\right)^{12} = \frac{55}{2^{11}}.
[/math]
La probabilità richiesta è perciò
p(10)+p(11)+p(12)= \frac{1}{2^9} + \frac{5}{2^9} + \frac{55}{2^{11}} = \frac{79}{2^{11}}.
[/math]
Quesito 9
Per verificare che
\overline{AB}=|B-A|=|(0,-2,2)|=\sqrt{2^2+2^2}=2\sqrt{2}.
[/math]
Analogamente otteniamo
\frac{A+B+C}{3}=\left(\frac{7}{3},\ \frac{1}{3},\ \frac{4}{3}\right).
[/math]
Un vettore perpendicolare ad
\begin{cases}
\frac{7}{3}+t\\
\frac{1}{3}+t\\
\frac{4}{3}+t
\end{cases}\quad t\in \mathbf{R}.
[/math]
Per stabilire quali sono i punti
\left(\frac{11}{3},\ \frac{5}{3},\ \frac{8}{3}\right) \quad \text{e} \quad (1,-1,0),
[/math]
che sono uno il simmetrico dell'altro rispetto al baricentro di
Quesito 10
Calcoliamo
y'(x)=2ke^{kx+2} \quad \text{e} \quad y''(x)=2k^2e^{kx+2}
[/math]
Sostituendo le due funzioni appena trovate nell'equazione differenziale
2k^2e^{kx+2}-2(2ke^{kx+2})-3(2e^{kx+2})=0
[/math]
cioè
(2k^2-4k-6)e^{kx+2}=0
[/math]
Il membro di sinistra dell'ultima equazione,
Affinché
La help line prima prova maturità 2018
Skuola.net sarà al fianco di tutti gli studenti che dovranno affrontare la maturità per aiutarli a superarla al meglio. Quindi niente panico: ci impegneremo a fugare ogni vostro dubbio e ogni vostra domanda, cercheremo di rispondervi velocemente e di aggiornarvi in tempo reale su tutto ciò che succede in questa Maturità 2018.
Ma tenete presente che le tracce e le soluzioni non potranno essere pubblicate fino al momento consentito dalla legge. Noi infatti non vogliamo farvi copiare e invalidare l' esame, ma supportarvi nel migliore dei modi. Durante lo svolgimento delle prove non risponderemo alla helpline per evitare di compromettere l'esame dei maturandi. Sempre per lo stesso motivo, le soluzioni non saranno in nessun caso disponibili prima del tempo stabilito per legge.
Per ogni informazione, dubbio o problema, ecco i nostri recapiti:
WhatsApp numero 3938835286
Chat di Facebook Messenger
2
Figura 1: Rappresentazione della mattonella relativa alla curva Λ
Punto 2
Dobbiamo costruire una mattonella che abbia
f (0) = 1
f (1) = 0
per
0 < f (x) < 1 0 < x < 1
′
f (0) = 0
∫
55
1 f (x)dx =
0 100 2
A nché un generico polinomio di secondo grado soddisfi le
f (x) = ax + bx + c
condizioni poste, dobbiamo avere
· ·
2
a 0 + b 0 + c = 1
· ·
2
a 1 + b 1 + c = 0
2
0 < ax + bx + c < 1 0 <x< 1
·
2a 0 + b = 0
∫
1 55
2
(ax + bx + c)dx = 100
0
Ricaviamo dunque
c =1
c =1
−1
a + b + c = 0 a =
b =0 b =0
]
[
1
2
3 x 11
x a b 11
+ b + cx =
a + + c =
3 2 20 3 2 20
0
A cura di:
C. Andreotti E. Bombardelli G. Dalla Torre M. Del Prete
L. Girella A. Osman C. Valsecchi L.Zeni 3
che è un sistema che non ammette soluzione. Non è quindi possibile realizzare
quanto richiesto con una funzione polinomiale di secondo grado.
Consideriamo ora una generica funzione polinomiale di terzo grado
3 2
f (x) = ax + bx + cx + d
e imponiamo le condizioni richieste:
· · ·
3 2
a 0 + b 0 + c 0 + d = 1
· · ·
3 2
a 1 + b 1 + c 1 + d = 0
3 2
0 < ax + bx + cx + d < 1 0 <x< 1
· ·
2
3a 0 + 2b 0 + c = 0
∫
55
1 3 2
(ax + bx + cx + d)dx =
0 100
Ricaviamo dunque
d =1 d =1
a + b + c + d = 0 a + b + 1 = 0
c =0 c =0
[ ]
11 11
1
4 3 2
x x x b c
a
a + b + c + dx = + + + d =
4 3 2 4 3 2
20 20
0
d = 1 d =1 d =1
−b − −b − −b − 7
a = 1 a = 1 a = 1 = 5
c =0 c =0 c =0
−b−1 −
3(−b−1)+4b+12
b 0 11 11 12
+ + +1= = b =
4 3 2 20 12 20 5
La funzione polinomiale di terzo grado che soddisfa le condizioni poste è quindi
12
7 −
3 2
f (x) = x x + 1 .
5 5
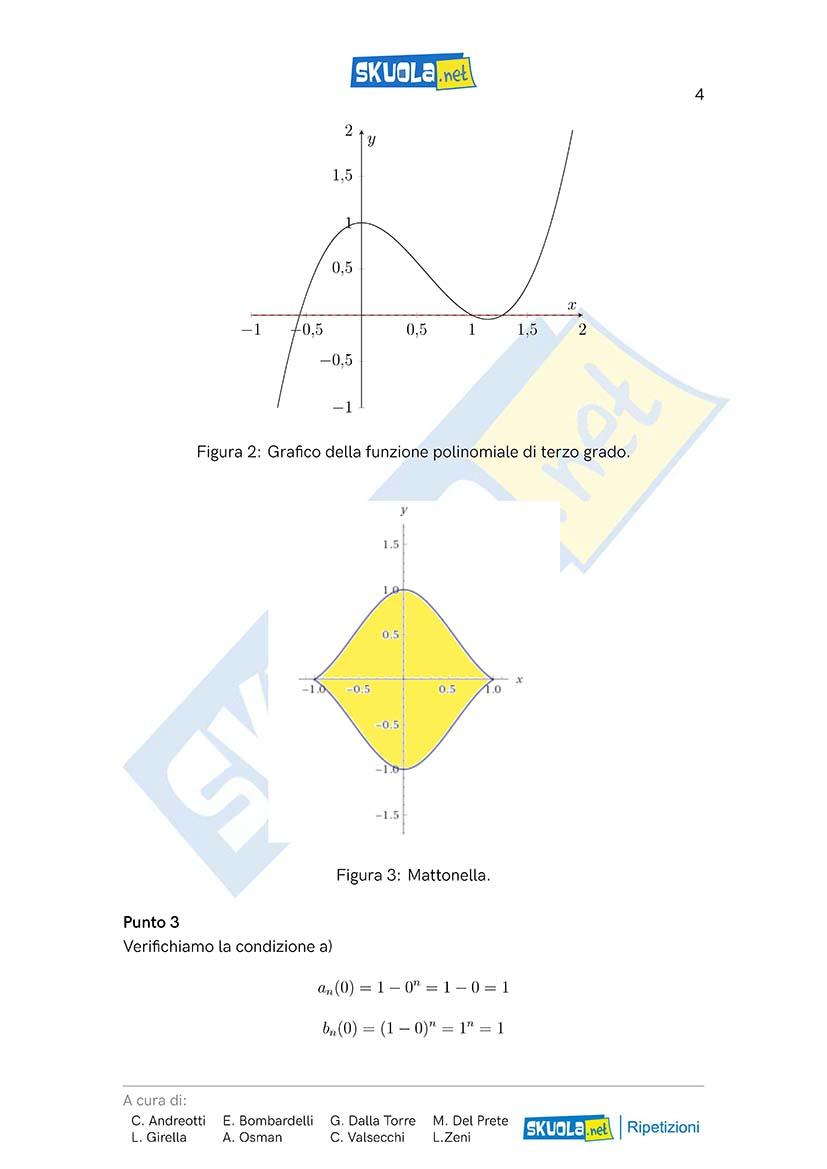
Per rappresentare la mattonella sul piano cartesiano studiamo la funzione f (x).
′
Sappiamo già che e che cioè il grafico di ha, per
f (0) = 1, f (1) = 0 f (0) = 0, f (x)
′ −
→ 24
21 2
+ ricaviamo
, tangente orizzontale. Studiando il segno di x x
x 0 f (x) = 5 5
′
che è strettamente negativa nell’intervallo In tale intervallo è
f (x) (0, 1]. f (x)
′′ −
42 24
quindi decrescente. Studiamo anche il segno di per vedere la
f (x) = x
5 5
concavità/convessità di La disuguaglianza
f (x). 24
42 − ≥
x 0
5 5 [ ]
≥ ∈
47 47
è soddisfatta per . Ne segue che è concava per , è convessa
x f (x) x 0,
[ ]
∈ 47 47
per e ha un punto di flesso a tangente obliqua in .
x , 1
A cura di:
C. Andreotti E. Bombardelli G. Dalla Torre M. Del Prete
L. Girella A. Osman C. Valsecchi L.Zeni 4
2 y
1,5
1
0,5 x
−1 −0,5 0,5 1 1,5 2
−0,5
−1
Figura 2: Grafico della funzione polinomiale di terzo grado.
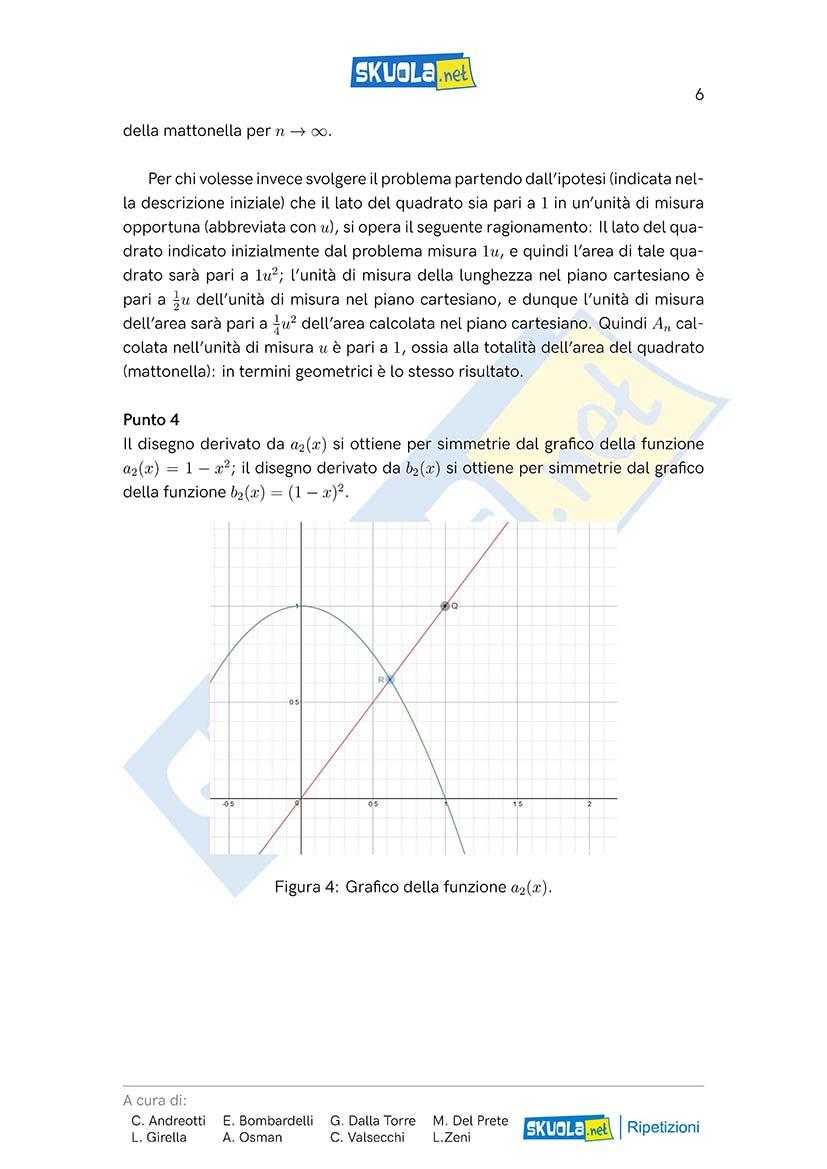
Figura 3: Mattonella.
Punto 3
Verifichiamo la condizione a) − −
n
a (0) = 1 0 = 1 0 = 1
n − n n
b (0) = (1 0) = 1 = 1
n
A cura di:
C. Andreotti E. Bombardelli G. Dalla Torre M. Del Prete
L. Girella A. Osman C. Valsecchi L.Zeni 5
Verifichiamo la condizione b) − −
n
a (1) = 1 1 = 1 1 = 0
n − n n
b (1) = (1 1) = 0 = 0
n
Verifichiamo la condizione c):
• per
0 < a (x) < 1 0 < x < 1:
n − n
0 < 1 x < 1
ovvero
− −x
n n n
1 x < 1 < 0 x > 0
− −x −1
n n n
1 x > 0 > x < 1
∀n ∈ N;
che è verificato per 0 < x < 1,
• per ovvero
0 < b (x) < 1 0 < x < 1:
n
√
− −x
−
n n 1=1
(1 x) < 1 < 0
1 x < √
−
− −x −1
n n
1 x > 0 = 0
(1 x) > 0 >
∀n ∈ N.
che è verificato per 0 < x < 1,
Siano ora e le aree delle parti colorate delle mattonelle, ovvero:
A B
n n [ [ ]
]
∫ ∫ 1
1 1 n+1 1
x
· · − − − −
n
A = 4 a (x)dx = 4 1 x dx = 4 x =4 1 0
n n n +1 n +1
0 0 0
−
n +1 1 n
A = 4 =4
n n +1 n +1 [ ]
∫ ∫ ∫ 1
−
1 1 1 n+1
(1 x)
−4· ·(−1)dx −4
n
n
(1−x) dx = (1−x) =
b (x)dx = 4·
B = 4·
n n n +1
0
0 0 0
[ ]
1 4
−4 −
B = 0 =
n n +1 n +1
→
Calcoliamo i limiti per n +∞: 4n
4n ( )
lim
lim lim = =4
A =
n 1
n + 1 n 1 +
n→+∞
n→+∞ n→+∞ n
4
lim lim
B = =0
n n + 1
n→+∞ n→+∞
L’area calcolata tende dunque al valore dell’intera area del quadrato (mat-
A
n
tonella), che nel piano cartesiano ha lato pari a e area pari a In termini
2 4.
geometrici, questo significa che la parte colorata tenderà a coprire l’intera area
A cura di:
C. Andreotti E. Bombardelli G. Dalla Torre M. Del Prete
L. Girella A. Osman C. Valsecchi L.Zeni 6
→ ∞.
della mattonella per n
Per chi volesse invece svolgere il problema partendo dall’ipotesi (indicata nel-
la descrizione iniziale) che il lato del quadrato sia pari a in un’unità di misura
1
opportuna (abbreviata con si opera il seguente ragionamento: Il lato del qua-
u),
drato indicato inizialmente dal problema misura e quindi l’area di tale qua-
1u,
2
drato sarà pari a ; l’unità di misura della lunghezza nel piano cartesiano è
1u
1
pari a dell’unità di misura nel piano cartesiano, e dunque l’unità di misura
u
2 14 2 dell’area calcolata nel piano cartesiano. Quindi cal-
dell’area sarà pari a u A
n
colata nell’unità di misura è pari a ossia alla totalità dell’area del quadrato
u 1,
(mattonella): in termini geometrici è lo stesso risultato.
Punto 4
Il disegno derivato da si ottiene per simmetrie dal grafico della funzione
a (x)
2
− 2 ; il disegno derivato da si ottiene per simmetrie dal grafico
a (x) = 1 x b (x)
2 2
− 2
della funzione .
b (x) = (1 x)
2 Figura 4: Grafico della funzione a (x).
2
A cura di:
C. Andreotti E. Bombardelli G. Dalla Torre M. Del Prete
L. Girella A. Osman C. Valsecchi L.Zeni 7
Figura 5: Grafico della funzione b (x).
2
Chiamiamo la probabilità che, se il braccio meccanico lascia cadere una
P a
goccia, questa causi il danneggiamento della mattonella e la stessa pro-
a (x), P
2 b
babilità per la mattonella Poiché la mattonella è simmetrica, possiamo
b (x).
2 ×
calcolare tali probabilità sul solo quadrato dunque avremo che:
[0, 1] [0, 1];
−
RQ OQ OR OR
−
P = = =1
a OQ OQ OQ
−
SQ OQ OS OS
−
P = = =1
b OQ OQ OQ
Calcoliamo quindi le coordinate dei punti e come interserzione tra i grafici
R S
e con la bisettrice
a (x) b (x) y = x:
2 2
− 2
y = 1 x
a (x) :
2
y = x
− 2
x = 1 x
−
2
x + x 1 = 0
√
−1 ± 5
x =
1,2 2
√
−1+ 5
di cui solamente la soluzione è interna al quadrato; quindi
x = R =
( ) 1 2
√
√ −1+
−1+ 5 5 .
,
2 2
A cura di:
C. Andreotti E. Bombardelli G. Dalla Torre M. Del Prete
L. Girella A. Osman C. Valsecchi L.Zeni 8
− 2
y = (1 x)
b (x) :
2 y = x
− 2
x = (1 x)
− 2
x = 1 2x + x
−
2
x 3x + 1 = 0
√
±
3 5
x =
1,2 2 ( )
√ √ √
3− 5 3− 5 3− 5
di cui solamente la soluzione è interna al quadrato; quindi .
x = S = ,
2 2 2 2
Le misure dei segmenti e saranno quindi rispettivamente:
OR OS
v
( (
) ( ) )
u √ √
√
u 2 2 √
−1 −1
−1
t + 5 5 + 5
+ 2
OR = + =
2 2 2
v ( ) ( ) ( )
u √ √ √
u 2 2 √
− − −
t 3 5 3 5 3 5
+ = 2
OS = 2 2 2
Inoltre la lunghezza del segmento essendo la diagonale di un quadrato
OQ,
√
di lato è pari a Quindi avremo che:
1, 2. )
(
√ √ √
−1+ 5
2 −1 5
OR +
2
√
− ≃
− − 0, 382
=1
P = 1 =1
a OQ 2
2
( )
√ 3−√ √
5
2 −
OS 3 5
2
√
− − − ≃
P = 1 =1 =1 0, 618
b OQ 2
2 20
In conclusione, poiché la probabilità di malfunzionamento è pari a ,
20% = 100
una ragionevole stima del numero totale di mattonelle danneggiate sarà:
20 · ·
N = (5000 P + 5000 P ) = 1000
a b
100
Problema 2
Punto 1
Le ordinate dei punti di tangenza delle rette e sono dati da:
r s
k k
• e dunque passa per
f (0) = 9 r P := (0, 9)
k k
• e dunque passa per
f (1) = k + 8 s Q := (1, k + 8)
k k
A cura di:
C. Andreotti E. Bombardelli G. Dalla Torre M. Del Prete
L. Girella A. Osman C. Valsecchi L.Zeni 9
Cerchiamo ora le equazioni delle rette tangenti e . Per determinare i coe -
r s
k k
cienti angolari, è su ciente calcolare la derivata prima nelle ascisse dei punti di
tangenza e
P Q: ′ −3x 2
(x) = + k
f k ′
m = f (0) = k
r k
k ′ −
m = f (1) = k 3
s k
k
L’equazione della retta è dunque
r
k − −
y y = m (x x )
P r P
k
−
y 9 = m x
r
k
y = kx + 9
e l’equazione della retta è
s k − −
y y = m (x x )
Q s Q
k
− − −
y (k + 8) = (k 3)(x 1)
−
y = (k 3)x + 11
Per trovare il punto di intersezione tra e è su ciente risolvere il sistema:
M s r
k k
y = kx + 9 y = kx + 9
− −
y = (k 3)x + 11 kx + 9(k 3)x + 11
2
y = kx + 9 y = k + 9
3
−3x 2
+ 11 = 9 x = 3
23
2
Dunque M ( , k + 9).
3
Punto 2
L’ordinata del punto può essere vista come una funzione del parametro
M k:
2 k + 9
M = M (k) =
y 3
Basta allora imporre alla funzione la condizione richiesta:
2 3
→
k + 9 < 10 k <
3 2
Poiché deve essere un numero intero positivo, il valore cercato è
k k = 1.
−x 3
Studiamo f (x) = + x + 9.
1
A cura di:
C. Andreotti E. Bombardelli G. Dalla Torre M. Del Prete
L. Girella A. Osman C. Valsecchi L.Zeni 10
R.
• Dominio: la funzione è polinomiale, perciò definita su tutto
√ √
′ −3x −
2
• Derivata prima: f (x) = + 1 = (1 + 3x)(1 3x)
1 √
± ± 3
1
√
– I punti stazionari sono: e le corrispondenti ordinate
x = =
1,2 3
3
√
± 2 3
sono date da y = f (x ) = +9
1,2 1 1,2 9 ′ ≥ ⇐⇒ −3x ≥
2
– Studiamo il segno della derivata prima f (x) 0 + 1 0
1
quindi, essendo un polinomio di grado 2, con coe ciente del termine
quadratico negativo, è rappresentabile da una parabola con concavità
rivolta verso il basso. Si può concludere che assuma valori nulli o posi-
√ √
≤ ≤ 3 2 3
tivi per . Possiamo inoltre concludere che
x x x A(− , + 9)
1 2 √ √ 3 9
−
3 3
2
è un punto di minimo relativo e di massimo relativo.
B( , + 9)
3 9
• Studio degli asintoti: essendo definita su tutto l’asse reale, i limiti vanno
studiati solo all’infinito. Calcoliamo: −∞
3
lim lim
f (x) = (−x + x + 9) =
1
x→∞ x→∞ 3
lim lim
f (x) = (−x + x + 9) = +∞
1
x→−∞ x→−∞
• Derivata seconda: cerchiamo eventuali punti di flesso calcolando la deri-
vata seconda, e ponendola uguale a 0:
′′ −6x, −6x
f (x) = = 0, x = 0.
1
Troviamo un punto di flesso poiché in la
F = (0, f (0)) = (0, 9), x = 0
1
derivata seconda cambia di segno.
A cura di:
C. Andreotti E. Bombardelli G. Dalla Torre M. Del Prete
L. Girella A. Osman C. Valsecchi L.Zeni 11
Figura 6: Grafico di f (x).
1
Punto 3
I vertici del triangolo richiesto sono:
• L’intersezione tra la retta e l’asse delle
r x: A(−9, 0)
1 11
• L’intersezione tra la retta e l’asse delle
s x: B( , 0)
1 2
29
23
• L’intersezione tra le rette e , cioè , )
r s M (
1 1 1 3
A cura di:
C. Andreotti E. Bombardelli G. Dalla Torre M. Del Prete
L. Girella A. Osman C. Valsecchi L.Zeni 12
Figura 7: Grafico relativo al punto 3 del problema.
La probabilità di scegliere un punto a caso in una sezione di una data regione
P
di piano è il rapporto tra l’area della sezione e l’area totale della regione.
Calcoliamo l’area del triangolo:
11 29 1
− · ·
A = ( (−9)) = 70.08
tot 2 3 2
Invece l’area della sezione voluta può essere ottenuta come di erenza tra la
regione totale, e: 9·9
• Area del triangolo :
AOP = 40.5
2
• Area sottesa dal grafico della funzione nell’intervallo dove è
f (x) [0, c], c
1
l’ascissa del punto d’intersezione tra e l’asse delle Per trovare
C f (x) x.
1
il valore di bisogna risolvere l’equazione che purtroppo ri-
c, f (c) = 0,
1
sulta cubica non scomponibile e quindi non risolvibile analiticamente con i
metodi studiati a scuola. Per stimare ci sono due alternative:
c ≈
– Utilizzando la calcolatrice grafica, si trova c 2.24.
A cura di:
C. Andreotti E. Bombardelli G. Dalla Torre M. Del Prete
L. Girella A. Osman C. Valsecchi L.Zeni 13
∈ 11
– Sfruttando il metodo di bisezione. Notando che si parte
c (1, )
2
11
con e Dunque:
f (1) > 0 f ( ) < 0.
2 segno di
x f (x)
−
11
4
11 +
8
33 +
16 −
77
32 ≈ ≈
77
Fermando l’iterazione a questo valore di otteniamo
x, c 2.41
32
Per il calcolo dell’area, si procede con l’integrale definito nell’opportuno inter-
vallo: ]
[
∫ c
c 2
4 x
x
−
3
I = (−x + x + 9)dx = + + 9x
4 2
0 0
≈ ≈ ≈ ≈
Nel caso di abbiamo Nel caso di abbiamo
c 2.24 I 16.37. c 2.41 I 16.16.
Quindi otteniamo la probabilità, nei due casi:
− −
70.08 40.5 16.37
P ≈
= 0.19
70.08
− −







 Accedi a tutti gli appunti
Accedi a tutti gli appunti
 Tutor AI: studia meglio e in meno tempo
Tutor AI: studia meglio e in meno tempo









