Anteprima
Vedrai una selezione di 1 pagina su 3
Disdici quando
vuoi
vuoi
Acquista con carta
o PayPal
o PayPal
Scarica i documenti
tutte le volte che vuoi
tutte le volte che vuoi
Sintesi
Ecco la traccia e la soluzione della seconda prova di matematica per la maturità 2014 del liceo scientifico.
Segui la diretta della Seconda Prova Maturità 2015: Tracce e Soluzioni
COMMENTI ALLE PROVE:
Il tema di matematica è sostanzialmente tutto concentrato sull'analisi, senza presentare alcuna richiesta di carattere esclusivamente geometrico o trigonometrico. Pertanto, la prova è perfettamente in linea con il programma riconosciuto dell'ultimo anno di liceo.
Problema 1: Tipico problema di analisi con lo studio di una funzione integrale. Vi sono molte richieste relative sia al calcolo differenziale (massimi, minimi, flessi), sia a quello integrale (volume del solido di rotazione). Il tutto a partire dal grafico della funzione da studiare.
Problema 2: Anche qui le richieste sono legate allo studio di una funzione di cui è già fornito il grafico. In particolare, vi sono alcune richieste sulla determinazione di massimi e minimi, una sul calcolo di un integrale per l'area e infine una richiesta di deduzione del grafico di una nuova funzione a partire da quella data.
Questionari:Sebbene vi siano richieste di ogni tipo, che spaziano dall'algebra all'analisi, passando per geometria analitica e trigonometria, nessuno dei questionari presenti mostra un particolare grado di complessità.
Problema 1
Punto a)
Osserviamo che
[math]g'(x)=f(x)[/math]
e pertanto [math]g'(0)=f(0)=0[/math]
in quanto [math]\Gamma[/math]
è tangente all'asse delle ascisse, mentre [math]g'(k)=f(k)=0[/math]
in quanto [math]x=k[/math]
è punto di massimo.Inoltre
[math]f[/math]
passa per i punti [math](0,0),\ (k,0)[/math]
ed avendosi [math]f'(x)=g''(x)[/math]
e [math]g''(h)=0[/math]
a causa della presenza del flesso e che[math]g''(x)<0\ x\in(h,w),\quad g''(x)>0,\ x\in(0,h)[/math]
segue che
[math]f[/math]
cresce su [math](0,h)[/math]
[math]f[/math]
decresce su [math](h,w)[/math]
[math]f[/math]
ha un massimo in [math]x=h[/math]
Avendosi pure
[math]f(x)>0\ \Leftrightarrow\ x\in(0,k)\\ f(x)<0\ \Leftrightarrow\ x\in(k,w)[/math]
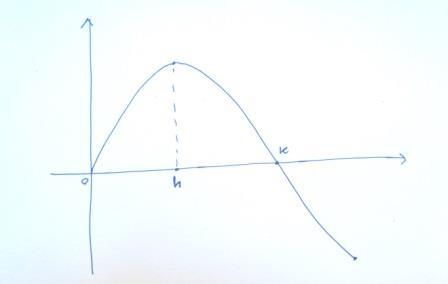
il grafico della funzione
[math]f[/math]
è il seguente:
Punto b)
Poniamo
[math]g(x)=ax^3+bx^2+cx+d[/math]
da cui
[math]g'(x)=3ax^2+2bx+c\\ g''(x)=6ax+2b[/math]
Abbiamo
[math]g(0)=0\ \Rightarrow\ d=0\\ g(w)=0\ \Rightarrow\ aw^2+bw+c=0\\ g'(0)=0\ \Rightarrow\ c=0\\ g'(k)=0\ \Rightarrow\ 3ak+2b=0\\ g''(h)=0\ \Rightarrow\ 6ah+2b=0[/math]
e quindi
[math]\left\{\begin{array}{l}
aw+b=0\\ 3ak+2b=0\\ 6ah+2b=0
\end{array}\right.[/math]
aw+b=0\\ 3ak+2b=0\\ 6ah+2b=0
\end{array}\right.[/math]
Sottraendo la terza dalla seconda si ha
[math]3ak-6ah=0\ \Rightarrow\ k=2h[/math]
, mentre, poiché dalla prima si ha [math]b=-aw[/math]
, sostituendo nella terza [math]6ah-2aw=0\ \Rightarrow\ w=3h[/math]
. Ciò mostra che l'intervallo [math][0,w][/math]
è suddiviso nei tre intervalli di uguale ampiezza [math][0,h],\ [h,2h],\ [2h,3h][/math]
.Punto c)
Se
[math]w=3[/math]
allora [math]h=1[/math]
. Inoltre abbiamo, da quanto visto in precedenza, [math]g(x)=ax^3+bx^2[/math]
. Ne segue che[math]g(1)=\frac{2}{3}=a+b\\ g(3)=0=27a+9b[/math]
e quindi dalla seconda
[math]b=-3a[/math]
che sostituito nella prima porta [math]a=-\frac{1}{3}[/math]
. In definitiva[math]g(x)=-\frac{1}{3} x^3+x^2[/math]
Poiché la funzione assume il valore cercato in
[math]x=1[/math]
abbiamo[math]-x^3+3x^2=2\ \Rightarrow\ x^3-3x^2+2=0[/math]
e potendo scomporre
[math]x^3-3x^2+2=(x-1)(x^2-2x-2)[/math]
si ricavano le ulteriori soluzioni
[math]x=1\pm\sqrt{3}[/math]
, delle quali risulta accettabile solo quella col segno positivo. I due punti sono allora[math]H(1,2/3),\quad P(1+\sqrt{3},2/3)[/math]
Poiché
[math]g'(x)=-x^2+2x[/math]
segue che i coefficienti angolari delle tangenti nei due punti sono rispettivamente [math]g'(1)=1,\qquad g'(1+\sqrt{3})=6+4\sqrt{3}[/math]
da cui le equazioni delle normali
[math]
y-\frac{2}{3}=-(x-1)\\ y-\frac{2}{3}=-\frac{1}{6+4\sqrt{3}}(x-1-\sqrt{3})[/math]
y-\frac{2}{3}=-(x-1)\\ y-\frac{2}{3}=-\frac{1}{6+4\sqrt{3}}(x-1-\sqrt{3})[/math]
Punto d)
Il volume del solido di rotazione intorno all'asse
[math]y[/math]
può essere visto come la somma infinita delle superfici laterali dei cilindri di raggio [math]x[/math]
e altezza [math]g(x)[/math]
al variare di [math]x[/math]
tra [math]a[/math]
e [math]b[/math]
, per cui si può esprimere il volume come [math]\int_{a}^{b}(2\pi)x\ g(x)\ dx[/math]
Abbiamo allora
[math]\int_0^3(2\pi x)\left(-\frac{1}{3}x^3+x^2\right)\ dx=2\pi\int_0^3\left(-\frac{x^4}{3}+x^3\right)\ dx=\\
2\pi\left[-\frac{x^5}{15}+\frac{x^4}{4}\right]_0^3\ dm^3=\frac{81\pi}{10}\ dm^3=\frac{81\pi}{10}\ litri[/math]
2\pi\left[-\frac{x^5}{15}+\frac{x^4}{4}\right]_0^3\ dm^3=\frac{81\pi}{10}\ dm^3=\frac{81\pi}{10}\ litri[/math]
Problema 2
Punto a)
Abbiamo
[math]f'(x)=\sqrt{4-x^2}+x\cdot\frac{-2x}{2\sqrt{4-x^2}}=\frac{4-x^2-x^2}{\sqrt{4-x^2}}=\frac{4-2x^2}{\sqrt{4-x^2}}=0[/math]
da cui i punti stazionari
[math]x=\pm\sqrt{2}[/math]
e quindi il massimo [math](\sqrt{2},4)[/math]
e il minimo [math](-\sqrt{2},4)[/math]
Punto b)
Poiché
[math]f(-x)=-x\sqrt{4-x^2}=-f(x)[/math]
la funzione risulta simmetrica rispetto all'origine. Inoltre
[math]f'(0)=2[/math]
e quindi l'angolo che la retta tangente forma con l'asse delle ascisse risulta pari a [math]\alpha=\arctan(2)\approx 63,43^\circ\approx 63^\circ 26'[/math]
Punto c)
La curva in questione è composta dai due rami della curva
[math]y=\pm f(x)[/math]
i quali coincidono con il grafico dato e con il suo simmetrico rispetto all'asse delle ascisse. L'area racchiusa da tale curva vale, pertanto, 4 volte l'area compresa sotto il grafico dato sull'intervallo [math][0,2][/math]
e quindi[math]A=4\int_0^2 f(x)\ dx=4\int_0^2 x\sqrt{4-x^2}\ dx=4\int_0^2 -\frac{1}{2}\cdot(-2x)\sqrt{4-x^2}\ dx=\\
-2\int_0^2\sqrt{4-x^2}\ d(4-x^2)=-2\cdot\frac{2}{3}\left[(4-x^2)^{3/2}\right]_0^2=\frac{32}{3}[/math]
-2\int_0^2\sqrt{4-x^2}\ d(4-x^2)=-2\cdot\frac{2}{3}\left[(4-x^2)^{3/2}\right]_0^2=\frac{32}{3}[/math]
Punto d)
Osserviamo che la funzione assume il valore 1 solo quando
[math]f(x)=\pi/2+k\pi,\ k\in\mathbb{Z}[/math]
. Tuttavia, poiché [math]f([0,2])=[0,4][/math]
, l'unico valore accettabile si ha per [math]f(x)=\pi/2[/math]
che ricade nell'immagine della funzione. Ne segue che[math]x\sqrt{4-x^2}=\frac{\pi}{2}\\ 4x^2(4-x^2)=\pi^2\\ 4x^4-16x^2+\pi^2=0[/math]
Risolvendo si trovano le soluzioni
[math]x^2_{1,2}=\frac{4\pm\sqrt{16-\pi^2}}{2}[/math]
entrambe positive e quindi le soluzioni accettabili
[math]x=\sqrt{\frac{4\pm\sqrt{16-\pi^2}}{2}}[/math]
I punti in cui
[math]h=1[/math]
sono massimi assoluti, mentre è facile vedere che non vi sono punti per cui [math]h=-1[/math]
in quanto dovrebbe aversi [math]f(x)=3\pi/2[/math]
che non appartiene all'immagine di cui sopra. Tuttavia [math]h'(x)=\cos(f(x))\cdot f'(x)[/math]
e si annulla o quando [math]x=\sqrt{2}[/math]
o quando [math]f(x)=\pi/2[/math]
. Questi ultimi due punti sono quelli appena calcolati in cui si ha massimo assoluto, mentre per il punto [math]x=\sqrt{2}[/math]
abbiamo un minimo relativo pari a [math]h(\sqrt{2})=\sin(f(\sqrt{2}))=\sin(2)>0[/math]
. Inoltre nei punti [math]x=0,\ x=2[/math]
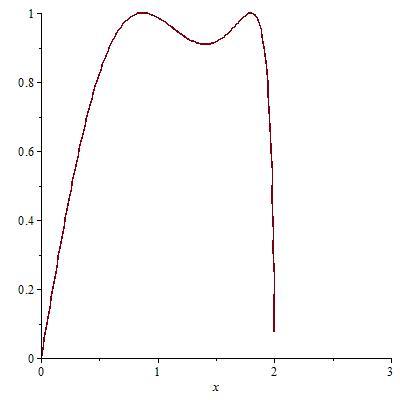
si hanno i minimi assoluti pari a zero. Osservando il grafico della funzione
[math]h[/math]
, si osserva che i valori di [math]k[/math]
per i quali si hanno 4 intersezioni sono quelli nell'intervallo [math](\sin(2),1)[/math]
Quesito 1
Sappiamo che in un triangolo qualunque vale la seguente relazione tra lati e angoli:
[math]\frac{a}{\sin\alpha} = \frac{b}{\sin\beta} = \frac{c}{\sin\gamma}[/math]
Nel nostro caso abbiamo:
[math]\frac{4}{\sin\alpha} = \frac{3}{\sin30^\circ}[/math]
[math]\Rightarrow\ \sin\alpha = \frac{4}{3}\sin 30^\circ = \frac{2}{3}\ \Rightarrow\ \alpha = \arcsin \frac{2}{3}\ approx 41^\circ 48'[/math]
Quesito 2
Esiste un teorema che assicura che la somma degli angoli che formano le facce di un angolo solido è minore di un angolo giro.
[math]\bullet[/math]
Notiamo che ad ogni vertice concorrono almeno 3 facce, e che la somma delle ampiezze degli angoli che concorrono in quel vertice deve essere minore di [math]360^\circ[/math]
Esistono quindi solo 5 poliedri regolari:
A) Tre hanno come facce triangoli rettangoli.
[math]\bullet[/math]
[math]3 \cdot 60^\circ = 180^\circ[/math]
TETRAEDRO REGOLARE[math]\bullet[/math]
[math]4 \cdot 60^\circ = 240^\circ[/math]
OTTAEDRO REGOLARE[math]\bullet[/math]
[math]5 \cdot 60 = 300^\circ[/math]
ICOSAEDRO REGOLAREB) Uno ha come facce quadrati:
[math]\bullet[/math]
[math]3 \cdot 90 = 180^\circ[/math]
CUBOC) Uno ha come facce pentagoni regolari:
[math]\bullet[/math]
[math]3 \cdot 108^\circ = 270^\circ[/math]
DODECAEDRO REGOLARED) Non esistono poliedri regolari che hanno come facce esagoni regolari: infatti si avrebbe
[math]3\cdot 120^\circ = 360^\circ[/math]
[IMPOSSIBILE]Quesito 3
[math](2a^2 - 3b^3)^n[/math]
Sviluppando compare il termine
[math]-1080a^4b^9[/math]
Vogliamo determinare il valore di n
Lo sviluppo della potenza di un binomio qualsiasi è dato da:
[math](a + b)^n = \sum_{k=0}^{n} \left(\begin{array}{c} n\\ k\end{array}\right) a^{n-k}b^k[/math]
Quindi otteniamo
[math]-1080a^4b^9[/math]
quando dovremo moltiplicare il quadrato di [math]2a^2[/math]
col cubo di [math]-3b^3[/math]
. Ciò implica che la somma degli esponenti dei termini (che è pari al valore cercato) risulta [math]n =2+3= 5[/math]
Quesito 4
Osserviamo che possiamo calcolare il volume attraverso la formula
[math]V=\int_{-2}^{-1} A(x)\ dx[/math]
dove
[math]A(x)[/math]
è l'area delle sezioni verticali del solido per ogni [math]x[/math]
fissato. Per calcolare tale area, è sufficiente notare che le sezioni risultano dei rettangoli di altezza [math]h(x)[/math]
e base [math]f(x)[/math]
e pertanto[math]V=\int_{-2}^{-1} A(x)\ dx=\int_{-2}^{-1} \frac{1}{x^2}\ e^{1/x}\ dx=[/math]
posto
[math]t=1/x\ \ dt=-1/x^2\ dx,\quad \ x=-1\to t=-1,\ x=-2\to t=-1/2[/math]
[math]V=\int_{-1/2}^{-1} -e^t\ dt=\left[-e^t\right]_{-1/2}^{-1}=-e^{-1}+e^{-1/2}=\frac{1}{\sqrt{e}}-\frac{1}{e}[/math]
Quesito 5
Vogliamo calcolare quanti sono i numeri tra 1 e 6000 non divisibili né per 2, né per 3, né per 5. Tra 1 e 6000 ci sono 3000 numeri divisibili per 2. A questi ne dobbiamo aggiungere 1000 divisibili per 3 (ma non anche per 2). Poi dobbiamo considerare quelli divisibili per 5 (ma non anche per 2 o per 3), che risultano essere 400. Quindi i numeri tra 1 e 6000 non divisibili né per 2, né per 3, né per 5 sono
[math]6000 - (3000 + 1000 + 400) = 6000 - 4400 = 1600[/math]
Quesito 6
Abbiamo un parallelepipedo a base quadrata di volume pari a 5 litri. Vogliamo minimizzare la superficie totale del solido sapendo che
[math]l^2 h = 5[/math]
litri = [math]5dm^3[/math]
, dove [math]l[/math]
è il lato del quadrato di base e [math]h[/math]
l'altezza del solido.Da:
[math]l^2 h = 5[/math]
ricaviamo [math]h = \frac{5}{l^2}[/math]
La funzione da minimizzare è
[math]f(l) = 2l^2 + 4 (l \cdot h) = 2l^2 + \frac{20}{l}[/math]
[math]f'(l) = 4l - \frac{20}{l^2} = \frac{4l^3 - 20}{l^3}=0[/math]
da cui
[math]l=\sqrt[3]{5}[/math]
che rappresenta il valore per cui si ha il minimo. Quesito 7
Il valore medio di
[math]f(x) = x^3[/math]
nell'intervallo chiuso [math][0, k][/math]
è 9. Cerco k:Per definizione di valor medio abbiamo:
[math]\frac{1}{k} \int_{0}^{k} x^3 dx = 9\ \Rightarrow\ \frac{1}{k} \left[\frac{x^4}{4}\right]_{0}^{k} = 9\ \Rightarrow\ k^3 = 36\ \Rightarrow k = \sqrt[3]{36} = 3,3019[/math]
Quesito 8
Sappiamo che un polinomio generico di quarto grado è della forma:
[math]P(x) = a_4x^4 + a_3x^3 + a_2x^2 + a_1x + a_0[/math]
Per ipotesi sappiamo che
[math]P(1) = 0 \Leftrightarrow a_4 + a_3 + a_2 + a_1 + a_0 = 0[/math]
[math]P(2) = 3 \Leftrightarrow 16a_4 + 8a_3 + 4a_2 + 2a_1 + a_0 = 3[/math]
[math]P(3) = 3 \Leftrightarrow 81a_4 + 27a_3 + 9a_2 + 3a_1 + a_0 = 3[/math]
[math]P'(2) = 0 \Leftrightarrow 32a_4 + 12a_3 + 4a_2 + a_1 = 0[/math]
[math]P'(3) = 0 \Leftrightarrow 108a_4 + 27 a_3 + 6 a_2 + a_1 = 0[/math]
Le ultime due le abbiamo perché per x=2 e x=3 P(x) ha il suo valore massimo. Ora risolvendo il sistema nelle sue 5 incognite otteniamo i coefficienti:
[math]a_4 = -\frac{3}{4} ;\ a_3 = \frac{15}{2} ;\ a_2 = -\frac{111}{4} ;\ a_1 = 45 ;\ a_0 = -24[/math]
Dunque possiamo calcolare:
[math] P(4) = -192 + 480 - 444 + 180 - 24 = 0[/math]
Quesito 9
[math]f(x) = \sqrt{3 - \log_2 (x + 5)}[/math]
Cerco il dominio di
[math]f(x)[/math]
, cioè risolvo il seguente sistema:[math]\left\{\begin{array}{l}
3 - \log_2 (x + 5) \geq 0\\
x + 5 > 0
\end{array}\right.[/math]
3 - \log_2 (x + 5) \geq 0\\
x + 5 > 0
\end{array}\right.[/math]
Dalla prima otteniamo che
[math]8\ge x+5\ \Rightarrow\ x\le 3[/math]
.Dalla seconda otteniamo che
[math]x>-5[/math]
.La soluzione è pertanto
[math]-5 < x \le 3\ \Rightarrow\ x\in(-5,3][/math]
.Quesito 10
Cerco: valori reali di x tali che
[math](\frac{1}{5} (x^2 - 10x + 26) )^{x^2 - 6x + 1} = 1[/math]
Affinché quest'espressione sia 1 deve accadere, o che la base sia 1 o che l'esponente sia zero, e cioè che:
[math]A:\quad x^2 - 10x + 26 = 5[/math]
[math]B:\quad x^2 - 6x + 1 = 0[/math]
Risolvo dunque queste due equazioni:
[math]A:\quad x^2 - 10x + 26 = 5\ \Rightarrow\ x^2 - 10x + 21 = 0\\ x = \frac{5 \pm \sqrt{25 - 21}}{1} = 5 \pm 2\ \Rightarrow\ x=3,\ x=7[/math]
[math]B:\quad x^2-6x+1=0\ \Rightarrow\ x=\frac{6\pm\sqrt{36-4}}{2}=3\pm 2\sqrt{2}[/math]
Estratto del documento
Pag. 2/3 Sessione ordinaria 2014
Seconda prova scritta
Ministero dell’Istruzione, dell’ Università e della Ricerca
–
M557 ESAME DI STATO DI LICEO SCIENTIFICO
CORSO DI ORDINAMENTO
Indirizzo: SCIENTIFICO
Tema di: MATEMATICA
PROBLEMA 2
A lato è disegnato il grafico della funzione
2
f x x 4 x
1. Si calcolino il massimo e il minimo
assoluti di .
f x
Si dica se l’origine O è centro di
2.
simmetria per e si calcoli, in gradi e
primi sessagesimali, l’angolo che la
tangente in O a forma con la direzione
positiva dell’asse x .
2 2 2
Si disegni la curva d’equazione l’area della parte di piano da essa
3. e si calcoli
y x 4 x
racchiusa.
4. Sia con . Quanti sono i punti del grafico di di ordinata 1? Il
h x sen f x h x
0 x 2
k
h x
grafico di presenta punti di minimo, assoluti o relativi? Per quali valori reali di
l’equazione ha 4 soluzioni distinte?
h x k
Dettagli
Accedi a tutti gli appunti
Tutor AI: studia meglio e in meno tempo
