1)
[math]A=\int_{\frac{1}{2}}^1\left(e^x-lnx\right)dx=\left[e^x-x\left(lnx-1\right)\right]_{\frac{1}{2}}^1=[/math]
[math]\left[e+1-e^{\frac{1}{2}}+\frac{1}{2}ln\frac{1}{2}-\frac{1}{2}\right]=[/math]
[math]e-e^{\frac{1}{2}}+\frac{1}{2}-\frac{1}{2}ln2[/math]
2)Se
[math]y=f(x),\ x=F(y)[/math]
sono una funzione inversa dell'altra, in modo che [math](x_0,y_0)[/math]
è il puntoper cui
[math]y_0=f(x_0),\ x_0=F(y_0)[/math]
, allora i volumi dei solidi di rotazione, rispettivamente rispetto all'assex e all'asse y si trovano usando gli integrali
[math]V_x=\pi\int_0^{x_0} [f(x)]^2\ dx,\qquad V_y=\pi\int_0^{y_0}[F(y)]^2\ dy.[/math]
Pertanto abbiamo
[math]V_x=\pi\int_0^{1/3}\left\{[g(x)]^2-[f(x)]^2\right\}\ dx,[/math]
[math]V_y=\pi\int_0^1\left\{[F(y)]^2-[G(y)]^2\right\}\ dy,[/math]
dove
[math]F,G[/math]
sono, rispettivamente, le funzioni inverse di [math]f,g[/math]
.3) r tangente a
[math]f\left(x\right):\; y=e^{x_0}\left(x-x_0\right)+e^{x_0}[/math]
s tangente a [math]g\left(x\right):\;y=\frac{1}{x_0}\left(x-x_0\right)+lnx_0[/math]
se [math]e^{x_0}=\frac{1}{x_0}[/math]
allora [math]s//r[/math]
[math]h\left(x\right)=e^x-\frac{1}{x}[/math]
[math]D\left(-\infty,0\right)\cup\left(0,+\infty\right)[/math]
sempre crescente.Per il teorema di esistenza degli zeri
[math]\exists ![/math]
la soluzione di [math]h\left(x\right)=0[/math]
Applicando la formula di Newton:[math]x_{n+1}=x_n-\frac{h\left(x_n\right)}{h'\left(x_n\right)}=x_n-\frac{e^{x_n}-\frac{1}{x_n}}{e^{x_n}+\frac{1}{x^2_n}}=[/math]
[math]\frac{e^{x_n}\left(x_n-1\right)+\frac{2}{x_n}}{e^{x_n}+\frac{1}{x^2_n}}[/math]
PUNTO INIZIALE [math]x_0=1[/math]
per [math]x_n=1[/math]
otterremo [math]x_{n+1}=0.538\; \Delta x=\left[x-x_{n+1}\right]0.562[/math]
posto dunque [math]x_n=0.538[/math]
, avremo [math]x_{n+1}=0.566[/math]
e dunque [math]\Delta x=\left[x_n-x_{n+1}\right]=0.028[/math]
L'approssimazione richiesta e' arrotondata ai centesimi, essendo [math]\Delta x=\frac{1}{100}[/math]
si dovrà continuare,ottenendo come soluzione
[math]x_n=0.566\; x_{n+1}=0.567\; \Delta x>\frac{1}{100}[/math]
pertanto la soluzione sara'[math]x\simeq0.566[/math]
4) La derivata prima di h(x) e' [math] h'(x) = e^x - \frac{1}{x} [/math]
Essa e' negativa per tutti i valori in cui [math] e^x - \frac{1}{x} > 0 \to e^x > \frac{1}{x} [/math]
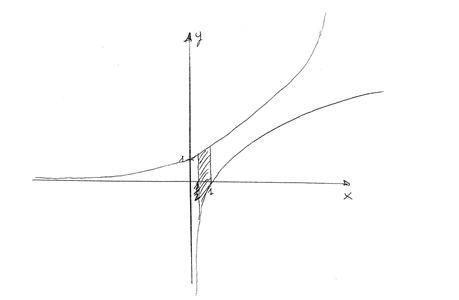
il valore, soluzione dell'equazione, e' un valore x0 compreso tra 1/2 e 1, in quanto la derivata per x=1/2 e' negativa mentre per x=1 e' positiva. pertanto nell'intervallo, x0 sara' il punto di minimo assoluto, mentre ai due estremi si trovera' uno dei due punti di massimo assolutoSostituendo ad h(x) i valori x=1/2 e x=1, si nota che il valore di h(x) e' maggiore per x=1 che pertanto sara' il punto di massimo assoluto
Accedi a tutti gli appunti
Tutor AI: studia meglio e in meno tempo
