1)I punti di flesso sono i punti in cui la derivata seconda di f si azzera. In relazione al grafico, dunque, saranno quei punti in cui f'(x) cambia monotonia (dove quindi la sua derivata si annulla), pertanto in
[math]x= 2[/math]
e
[math]x=4[/math]
, avremo due flessi.
Infatti calcolando il rapporto incrementale destro e sinistro, avremo nei punti in cui la funzione derivata prima presenta massimo e minimo:
[math]\frac{f'(x) - f'(4)}{x - 4}[/math]
Per x 4 il numeratore sarà sempre positivo, mentre il denominatore cambia segno, per cui il rapporto incrementale cambia segno e pertanto cambia la concavità analogamente si dimostra tramite il rapporto incrementale
[math]\frac{f'(x) - f'(2)}{x - 2}[/math]
si conclude che x = 2 è un altro punto di flesso.
2)Il minimo assoluto di f si ha dove la derivata si azzera, valutando però dove prima decresce (f'0), pertanto il minimo assoluto si avrà per x = 5
[math]\int_{0}^{6} f' (t) dt = - 5 \to f(6) - f(0) = -5[/math]
ma
[math]f(0) = 9[/math]
per ipotesi, quindi:
[math]f(6) - 9 = -5 \to f(6) = 4[/math]
, pertanto (0,9) è il punto di massimo assoluto avendo calcolato grazie all'integrale che f(0) > f(6);
il punto (6,4) è punto di massimo relativo.
3)Dominio:
[math]0 \leq x \leq 6[/math]
Intersezioni con gli assi:
[math]asse y: x = 0 , \ y =9[/math]
Punti: A (0,9) B (3,6) C(5,3)
Crescenza:
[math]5 \leq x \leq 6[/math]
Decrescenza
[math]0 \leq x \leq 5[/math]
x = 5 MINIMO
A (6,4) MASSIMO
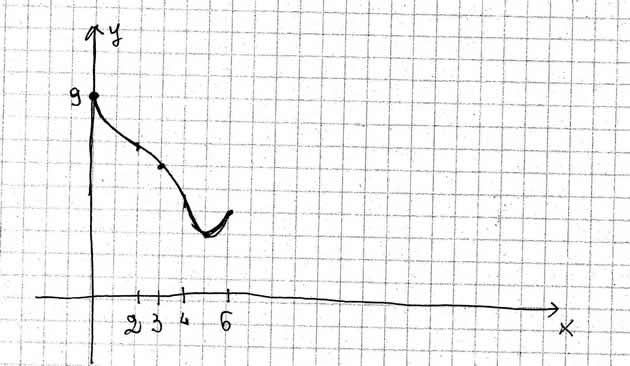
4)La tangente A f(x) in x=3 (e quindi y=6), essendo dal grafico f(3) = -1, avremo:
[math]y - y_0 = m (x -x_0)[/math]
La retta tangente:
[math]y - 6 = -1 (x - 3)[/math]
da cui
[math]y = - x + 9[/math]
[math]g (3) = 3f(3) = 3 \cdot 6 = 18[/math]
ed essendo:
[math]g(x) = x \ f(x)[/math]
sarà
[math]g'(x) = 1 - f(x) + x \ f'(x)[/math]
e dunque:
[math]g'(3) = f(3) + 3 \ f'(3) = 6 + 3 (-1) = 3[/math]
E dunque la retta tangente:
[math]y - 18 = 3(x - 3) \to y - 18 = 3x - 9 \to y = 3x + 9[/math]
L'angolo che l'intersezione tra le due rette genera sarà:
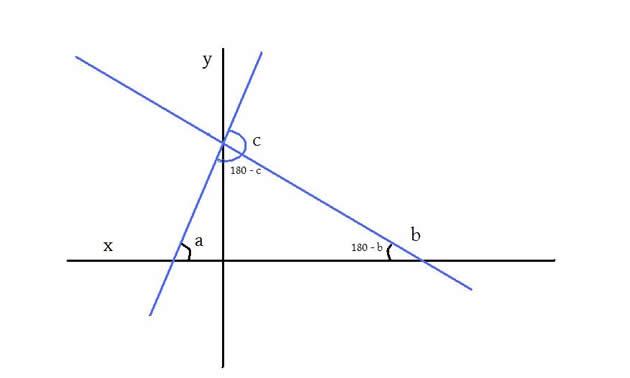
[math]\tan b = - 1[/math]
[math]tan a = 3[/math]
[math]\not{180} - b + a + 180 - c = \not{180}[/math]
[math]c = 180 + a - b[/math]
[math]\tan c = \tan (180 + a - b) = \\ = \tan ( a - b) = \\ = \frac{\tan a - \tan }{1 + \tan x + \tan b} = [/math]
[math]\frac{3 + 1}{1 - 3} = - 2[/math]








 Accedi a tutti gli appunti
Accedi a tutti gli appunti
 Tutor AI: studia meglio e in meno tempo
Tutor AI: studia meglio e in meno tempo