Daniele
di Daniele Grassucci
Immagine autore
2' di lettura 2' di lettura
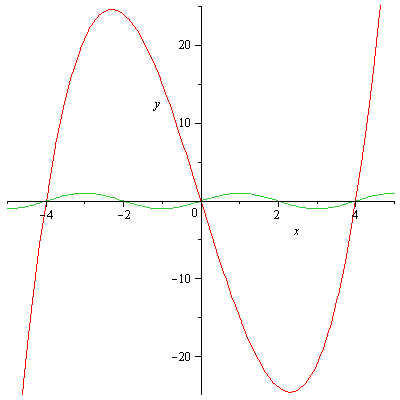
Matematica - Problema 2 - PNI (Soluzione) articoloEcco i grafici:

Il disegno viene immediatamente considerando che

[math]\sin x[/math]
è una funzione nota, e che
[math]f(x) = x^3 - 16x[/math]
ha gli zeri in
[math]x=0,\pm 4[/math]

La derivata è

[math]f'(x) = 3x^2 - 16[/math]
.
I punti di massimo e minimo sono

[math]\left(\pm \frac{4}{\sqrt{3}}; \mp \frac{128}{3\sqrt{3}} \right)
[/math]

Per quanto riguarda g, i massimi e minimi in [-10,10] sono

[math]\left(1;1\right),\left(5;1\right),\left(9;1\right),\left(-3;1\right),\left(-5;1\right),\left(-7;1\right),\\
\left(3;-1\right),\left(7;-1\right),\left(-1;-1\right),\left(-5;-1\right),\left(-7;-1\right)= \left(2k + 1;\left(-1\right)^k\right), k \in \left[-10;10\right] \cap \mathbb{Z}[/math]

L'area di R è data da

[math]\int_0^4 g(x)dx + \int_4^0 f(x)dx = \int_0^4 \sin \frac{\pi}{2}x dx
+ \int_4^0 \left(x^3 - 16x\right) dx =\\
= \left. \frac{x^4}{4} - 8x^2 \right|_4^0 = - 64 + 128 = 64[/math]

Calcoliamo le intersezioni di f con le rette y = -15 e y = -5. Con la prima otteniamo le soluzioni esatte

[math]x^3 - 16x + 15 = 0 \Rightarrow x = 1, \frac{\sqrt{61}- 1}{2} \simeq 3.40[/math]
Per la seconda si procede col metodo delle tangenti. Partendo da x = 0, si ottiene:
[math]x_1 = 0 - \frac{5}{-16} =0.3125\\
x_2 = 0.3125 - \frac{10.03}{-15.75}=.3144[/math]
L'altra soluzione si ottiene partendo da 4

[math]x_1 = 4 - \frac{64 - 64 + 5}{48 - 16} =0.384375\\
x_2 = .38335[/math]

Per il volume, bisogna calcolare:

[math]\int_0^4 \left[ g(x) - f(x) \right](5-x) dx=\\
= \int_0^4 \sin \frac{\pi}{2}x (5 - x)dx + \int_0^4 \left(x^4 - 5x^3 - 16x^2 + 80x\right) =\\
\left. -\frac{2}{\pi} \cos \frac{\pi}{2}x (5 - x) \right|_0^4 - \int_0^4 \cos \frac{\pi}{2}x dx + \left[\frac{x^5}{5} - \frac{5x^4}{4} - \frac{16x^3}{3} + 40x^2\right]_0^4 = \\
= \frac{8}{\pi} + 4^3 \frac{43}{15} \simeq 186
[/math]
In litri si tratta di 186.000 litri