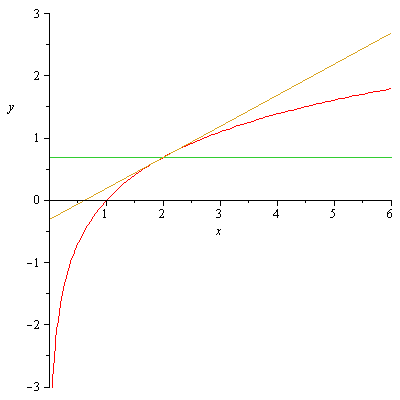
1)
Ogni punto appartentente alla funzione ha coordinate generiche
L'equazione della retta generica, passante per un punto
e tangente ad una funzione
ha equazione generica
e pertanto, per quanto detto sopra, la retta t del caso avra' equazione
Il punto A, di ascissa nulla, avra' coordinate
E il punto B, avra' anch'esso ascissa nulla e ordinata a quella del punto P generico.
Il segmento AB, segmento a cui appartengono due punti aventi stessa ascissa, avrà lunghezza pari alla differenza delle ordinate (in valore assoluto) ovvero
E dunque il segmento AB sara' costante e uguale a 1.
Per la seconda parte, si procede in maniera analoga.
La retta t si ricava dalla relazione
E pertanto
E i punti A e B avranno rispettivamente coordinate generiche
Da cui, la distanza AB sara'
, che varia a seconda del valore di a.
2)Il punto di ascissa 1 ha ordinata 0.
La pendenza del del piano
sarà data sia dalla derivata prima della funzione nel punto in esame che dalla tangente dell'angolo.
Pertanto
Ovvero
Che risolta, darà
Nel caso di
avremo
Da cui
3)
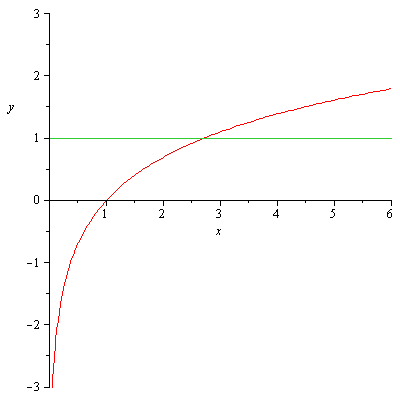
Detto Q il punto di intersezione tra la funzione e la retta y=1,Q' la proiezione di Q sull'asse delle ascisse, R e O i punti di intersezione tra l'asse y e rispettivamente le rette y=1 e y=0, l'Area D richiesta dal problema sarà data dall'area del rettangolo RQQ'O - l'area sottesa dalla funzione.
Sapendo che le coordinate dei punti sono
e
L'area del rettangolo sara' data da
mentre l'area della regione sara'
integrando per parti
E pertanto l'area di D sara'
4)
da cui
Il centro di rotazione e' sull'asse x=-1 (lavorando sulla funzione inversa) pertanto trasliamo di +1 per avere asse di rotazione x=0.
Otteniamo cosi' la funzione
dove
è il volume del cilindro di raggio=1 e altezza = 1.



 Accedi a tutti gli appunti
Accedi a tutti gli appunti
 Tutor AI: studia meglio e in meno tempo
Tutor AI: studia meglio e in meno tempo