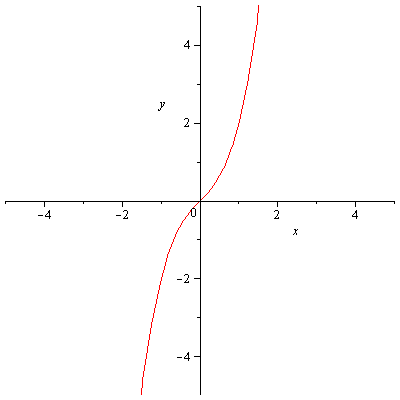
Sia
[math]f:\mathbb{R}\rightarrow\mathbb{R}[/math]
, definita da
[math]f(x)=x^3+kx[/math]
, con
[math]k\in\mathbb{R}[/math]
Punto 1)
Il dominio della funzione è tutto l'asse reale. Inoltre
[math]f(0)=0[/math]
mentre
[math]f(x)\ge 0\Leftrightarrow x(x^2+k)\ge 0[/math]
e si ha
a) se
[math]k>0[/math]
, per
[math]x\ge 0[/math]
;
b) se
[math]k=0[/math]
, per
[math]x\ge 0[/math]
;
c) se
[math]k>0[/math]
, per
[math]-\sqrt{-k}\le x\le 0,\ x\ge\sqrt{-k}[/math]
.
Inoltre
[math]\lim_{x\rightarrow\pm\infty} f(x)=\pm\infty[/math]
e sono indipendenti da
[math]k[/math]
.
Si ha poi
[math]f'(x)=3x^2+k\ge 0[/math]
e quindi
a) se
[math]k>0[/math]
, per
[math]x\in\mathbb{R}[/math]
;
b) se
[math]k=0[/math]
, per
[math]x\in\mathbb{R}[/math]
;
c) se
[math]k>0[/math]
, per
[math]x\le-\sqrt{-k/3},\ x\ge\sqrt{-k/3}[/math]
.
Nel caso c) si hanno allora due estremi:
un Max in
[math]x=-\sqrt{-k/3}[/math]
che vale
[math]-\frac{2k}{3}\sqrt{-\frac{k}{3}}[/math]
;
un min in
[math]x=\sqrt{-k/3}[/math]
che vale
[math]\frac{2k}{3}\sqrt{-\frac{k}{3}}[/math]
.
Infine
[math]f''(x)=6x\geq 0[/math]
per
[math]x\geq 0[/math]
e quindi si ha un flesso in
[math]x=0[/math]
.
Il grafico nei tre casi è riportato di seguito:
a)
[math]k>0[/math]
b)
[math]k=0[/math]
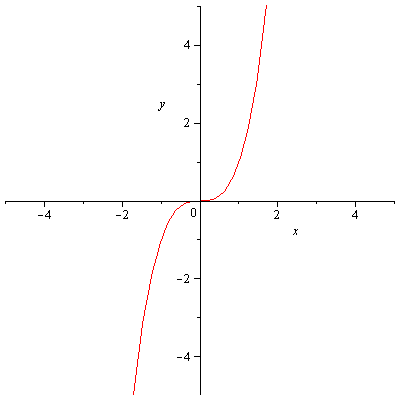
c)
[math]k>0[/math]
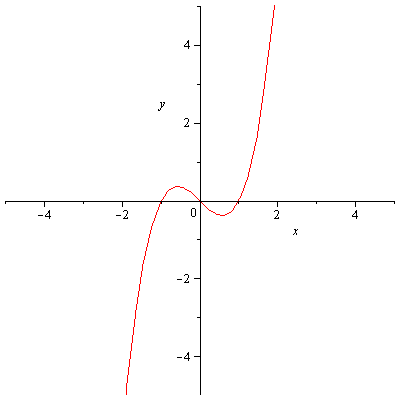
Si osservi che la differenza nel grafico in a) e b) sta nella pendenza (la tangente nell'origine.
Punto 2)
Consideriamo
[math]g(x)=x^3[/math]
la cui intersezione con
[math]y=1-x[/math]
si ottiene risolvendo
[math]x^3=1-x[/math]
.
Considero la funzione
[math]h(x)=x^3+x-1[/math]
, che ha dominio coincidente con l'asse reale e per cui
[math]\lim_{x\rightarrow\pm\infty} h(x)=\pm\infty[/math]
. Inoltre
[math]h'(x)=3x^2+1>0[/math]
per ogni valore reale, e quindi
[math]h(x)[/math]
è ovunque crescente. Dal teorema di esistenza degli zeri esiste allora un unico
[math]c\in\mathbb{R}[/math]
tale che
[math]h(c)=0[/math]
e quindi
[math]g(c)=1-c[/math]
per un unico punto c.
Punto 3)
La funzione inversa è data da
[math]y=\sqrt[3]{x}[/math]
e quindi dobbiamo calcolare l'integrale della regione finita illustrata in figura (compresa tra i due archi).
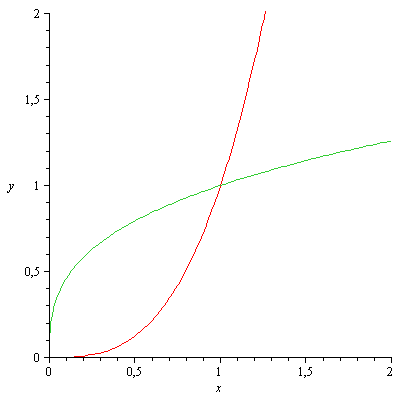
Per determinare il punto di intersezione, dobbiamo risolvere
[math]\sqrt[3]{x}=x^3[/math]
, da cui
[math]x-x^9=0[/math]
le cui uniche soluzioni reali e non negative sono
[math]x00,\ x=1[/math]
. Allora
[math]D=\int_0^1[\sqrt[3]{x}-x^3]\ dx=\int_0^1[x^{1/3}-x^3]\ dx[/math]
[math]=\left[\frac{3}{4}\ x^{4/3}-\frac{x^4}{4}\right]_0^1=\frac{3}{4}-\frac{1}{4}=\frac{1}{2}[/math]
Punto 4)
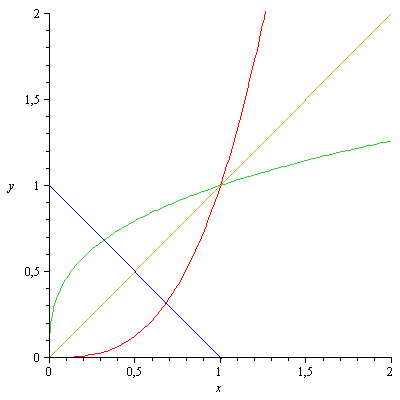
Per calcolare il volume, osserviamo che ogni rettangolo ha la base che risulta perpendicolare alla bisettrice del primo quadrante. La metà di tale base è pari alla distanza del punto
[math]p(\alpha,\alpha^3)[/math]
generico sulla curva
[math]g(x)[/math]
e la bisettrice stessa. Allora
[math]\frac{b}{2}=\frac{|\alpha-\alpha^3|}{\sqrt{2}}[/math]
ed essendo
[math]0\le\alpha\le 1[/math]
e quindi
[math]\alpha-\alpha^3\ge 0[/math]
si ha
[math]b(\alpha)=\frac{2(\alpha-\alpha^3)}{\sqrt{2}}[/math]
Allora
[math]A(\alpha)=h\cdot b(\alpha)=12\sqrt{2}(\alpha-\alpha^3)[/math]
.
Avendosi
[math]A'(\alpha)=12\sqrt{2}(1-3\alpha^2)=0\Leftrightarrow \alpha=1/\sqrt{3}[/math]
risulta l'unico punto accettabile e rappresenta il massimo che vale
[math]A(1/\sqrt{3})=12\sqrt{2}\cdot\frac{1}{\sqrt{3}}(1-1/3)=\frac{8\sqrt{6}}{3}[/math]
.
Per il volume abbiamo
[math]W=\int_0^1 A(\alpha)\ d\alpha=12\sqrt{2}\int_0^1[\alpha-\alpha^3]\ d\alpha[/math]
[math]=12\sqrt{2}\left[\frac{\alpha^2}{2}-\frac{\alpha^4}{4}\right]_0^1[/math]
[math]=12\sqrt{2}\left(\frac{1}{2}-\frac{1}{4}\right)=3\sqrt{2}[/math]
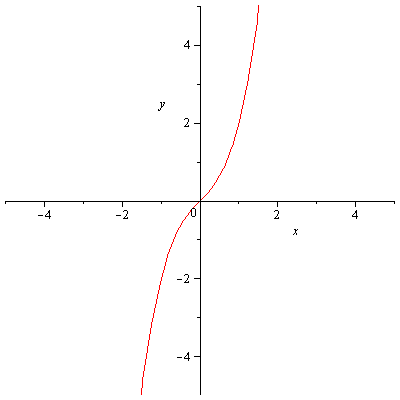
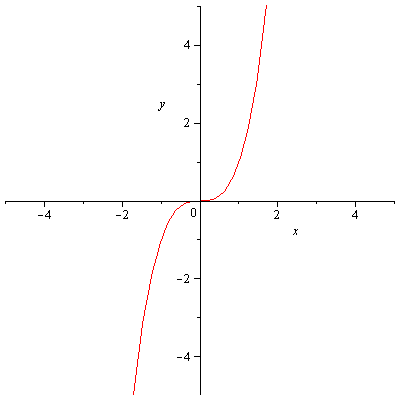
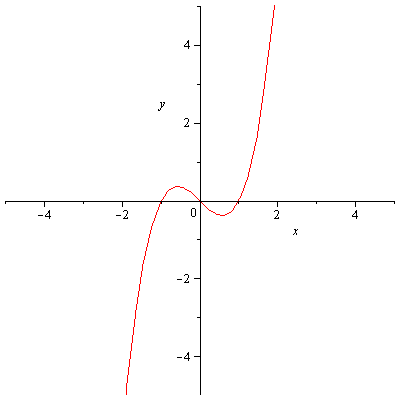
Accedi a tutti gli appunti
Tutor AI: studia meglio e in meno tempo
