In una circonferenza di raggio
[math]r[/math]
due corde consecutive [math]AB[/math]
e [math]AC[/math]
hanno lunghezza rispettivamente [math]r/3[/math]
e [math]2/3 r [/math]
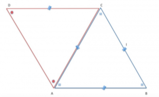
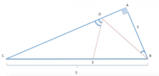
. Calcolare l'area del triangolo [math]ABC[/math]
.
Svolgimento
Dal teorema della corda, secondo il quale, in una circonferenza, ogni corda è uguale al prodotto del diametro per il seno dell'angolo ad essa opposto, possiamo trovare il lato[math]AC[/math]
:
[math] AC = 2r \cdot \sin (\beta) [/math]
Sapendo che
[math]AC = 2/3 r [/math]
, sostituiamo questo valore all'uguaglianza precedente:
[math] 2/3 r = 2r \cdot \sin (\beta) [/math]
Semplifichiamo:
[math] 2/3 = 2 \cdot \sin (\beta) [/math]
[math] 2 = 6 \sin (\beta) \to \sin (\beta) = 2/6 = 1/3 [/math]
Ora applichiamo il teorema dei seni: in un triangolo qualunque il rapporto fra la misura di un lato ed il seno dell'angolo opposto è costante, quindi:
[math]\frac{AC}{\sin(\beta)} = \frac{AB}{\sin(\hat{C})}[/math]
Ricaviamo ora
[math]\sin (\hat{C})[/math]
:
[math] \sin (\hat{C}) \cdot AC = AB \cdot \sin(\beta) [/math]
[math] \sin (\hat{C}) = \frac {AB \cdot \sin(\beta)}{AC} [/math]
Sostituiamo i valori che abbiamo:
[math] \sin (\hat{C}) = \frac{r/3 \cdot 1/3}{2/3 r} = r/9 \cdot 3/(2r) = 1/6 [/math]
Ora, poiché la somma degli angoli interni di un triangolo è
[math]180°[/math]
, sappiamo che:
[math] \hat{A} = 180° - (\hat{B} + \hat{C}) [/math]
Determiniamo ora il valore di
[math] \sin (\hat{A}) [/math]
:
[math] \sin (\hat{A}) = \sin[ 180° - (\hat{B} + \hat{C})] [/math]
Applichiamo la formula di sottrazione del seno:
[math] \sin \left[ 180^\circ - (\hat{B} + \hat{C}) \right] = \sin(180^\circ) \cos(\hat{B} + \hat{C}) - \cos(180^\circ) \sin(\hat{B} + \hat{C}) [/math]
[math] 0 \cdot \cos(\hat{B} + \hat{C}) - (-1) \sin(\hat{B} + \hat{C}) = \sin(\hat{B} + \hat{C})[/math]
Quindi:
[math] \sin (\hat{A}) = \sin (\hat{B} + \hat{C}) [/math]
Applichiamo la formula di addizione del seno:
[math]\sin (\hat{B} + \hat{C}) = \sin(\hat{B}) \cos(\hat{C}) + \cos(\hat{B}) \sin(\hat{C}) [/math]
Precedentemente, avevamo trovato i valori di
[math] \sin (\hat{C}) = 1/6 [/math]
e [math] \sin (\beta) = 1/3 [/math]
; troviamo i valori del coseno mediante la relazione fondamentale:
[math] \cos(\beta) = \sqrt{1 - \sin^2(\beta)} = \sqrt{1 - \left(\frac{1}{3}\right)^2} = \sqrt{1 - \frac{1}{9}} = \sqrt{\frac{8}{9}} = \frac{2\sqrt{2}}{3}[/math]
[math] \cos(\hat{C}) = \sqrt{1 - \sin^2(\hat{C})} = \sqrt{1 - \left(\frac{1}{6}\right)^2} = \sqrt{1 - \frac{1}{36}}[/math]
[math]\sqrt{\frac{35}{36}} = \frac{\sqrt{35}}{6} [/math]
Possiamo trovare
[math]\sin(\hat{A})[/math]
:
[math]\sin(\hat{A}) = \sin(\hat{B}) \cos(\hat{C}) + \cos(\hat{B}) \sin(\hat{C})[/math]
[math]\frac{1}{3} \cdot \frac{\sqrt{35}}{6} + \frac{2\sqrt{2}}{3} \cdot \frac{1}{6} = \frac{\sqrt{35}}{18} + \frac{\sqrt{2}}{9} = \frac{\sqrt{35} + 2\sqrt{2}}{18}[/math]
Per determinare l'area del triangolo
[math]ABC[/math]
moltiplichiamo i lati [math]AC[/math]
e [math]AB[/math]
per il seno dell'angolo fra essi compreso, dividendo poi per due:
[math]A_(ABC) = 1/2 * AB * AC * \sin(\hat{A}) = 1/2 * r/3 * 2/3 r * \frac{\sqrt{35} + 2\sqrt{2}}{18} = [/math]
[math] \frac{\sqrt{35} + 2\sqrt{2}}{162} r^2 [/math]
Accedi a tutti gli appunti
Tutor AI: studia meglio e in meno tempo
