Risolvere la seguente disequazione goniometrica:
[math]\\sin ^2(x/2) - (\sqrt3 - 1) \\sin{x/2} \\cos{x/2} - \sqrt3 \\cos^2{x/2} ≤ 0 [/math]
Svolgimento
Risolviamo la disequazione dividendo entrambi i membri per
[math]\\cos^2(x/2)[/math]
:
[math] frac(\\sin ^2(x/2) - (\sqrt3 - 1) \\sin{x/2} \\cos{x/2} - \sqrt3 \\cos^2{x/2})(\\cos^2{x/2}) ≤ 0 [/math]
Poniamo le condizioni di esistenza:
[math] \\cos^2(x/2) ≠0 \to \\cos(x/2) ≠0 \to x/2 ≠π/2 + kπ \to [/math]
[math] x ≠π + 2kπ [/math]
Ora risolviamo la disequazione:
[math] frac(\\sin ^2(x/2))((\\cos^2(x/2))) - frac((\sqrt3 - 1) \\sin{x/2} \\cos{x/2})((\\cos^2{x/2})) - frac(\sqrt3 \\cos^2{x/2})(\\cos^2{x/2}) ≤ 0[/math]
[math] frac(\\sin ^2(x/2))((\\cos^2(x/2))) - frac((\sqrt3 - 1) \\sin{x/2})((\\cos{x/2})) - \sqrt3 ≤ 0 [/math]
Trasformiamo in tangente:
[math] tg^2(x/2) - (\sqrt3 - 1) tg{x/2} - \sqrt3 ≤ 0 [/math]
Passiamo all'equazione associata:
[math] tg^2(x/2) - (\sqrt3 - 1) tg{x/2} - \sqrt3 = 0 [/math]
Determiniamo le soluzioni:
[math] tg(x/2) = frac(-b ± \sqrt{b^2 - 4ac})(2a) = frac( \sqrt3 - 1 ± \sqrt((\sqrt3 - 1)^2 - 4 \cdot (-\sqrt3)))(2) =[/math]
[math]frac( \sqrt3 - 1 ± \sqrt{ 3 + 1 - 2\sqrt3 + 4\sqrt3})(2) = frac( \sqrt3 - 1 ± \sqrt( 3 + 1 + 2\sqrt3))(2)[/math]
Notiamo che sotto radice abbiamo il quadrato svolto di un binomio:
[math] frac( \sqrt3 - 1 ± \sqrt{(\sqrt3 + 1)^2})(2) = frac( \sqrt3 - 1 ± (\sqrt3 + 1))(2) [/math]
Abbiamo quindi:
[math] tg_1 (x/2) = frac( \sqrt3 - 1 + {\sqrt3 + 1})(2) = frac( \sqrt3 - 1 + \sqrt3 + 1)(2) = [/math]
[math] frac(2\sqrt3){2} = \sqrt3 [/math]
[math] tg_2 (x/2) = frac( \sqrt3 - 1 - {\sqrt3 + 1})(2) = frac( \sqrt3 - 1 - \sqrt3 - 1)(2) = [/math]
[math] frac(-2)(2) = -1 [/math]
Essendo la disequazione minore o uguale a zero, prendiamo come soluzioni gli intervalli interni alle radici dell'equazione associata:
[math] -1 ≤ tg(x/2) ≤ \sqrt3 [/math]
Rappresentiamo la situazione sulla circonferenza goniometrica:
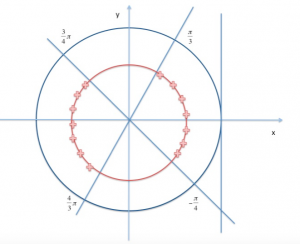
Avremmo quindi che:
[math] - π/4 + kπ ≤ x/2 ≤ π/3 + kπ [/math]
Moltiplicando per due otteniamo l'intervallo di x:
[math] - π/2 + 2kπ ≤ x ≤ 2/3 π + 2kπ [/math]
Accedi a tutti gli appunti
Tutor AI: studia meglio e in meno tempo
