Calcolare il perimetro e l'area di un triangolo rettangolo, sapendo che
[math]a=50cm[/math]
e [math]\\sin (gamma)=(24)/(25)[/math]
. Svolgimento
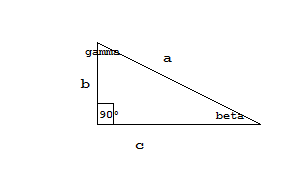
Dati
[math]a=50cm[/math]
[math]\\sin (gamma)=(24)/(25)[/math]
[math]alpha=90^circ[/math]
In un triangolo rettangolo un cateto è uguale al prodotto dell'ipotenusa
per il seno dell'angolo opposto al cateto stesso.
[math]c=a\\sin (gamma)=50cm(24)/(25)=48cm[/math]
;Pertanto il cateto maggiore misura
[math]=48cm[/math]
.Per il Teorema di pitagora
[math]b=\sqrt{a^2-c^2}=\sqrt((50cm)^2-(48cm)^2)=\sqrt((2500cm^2)-(2304cm^2))=\sqrt(196)cm=13cm[/math]
.Pertanto il perimetro del triangolo, dato dalla somma dei lati
[math]2p=a+b+c=(50+48+13)cm=112cm[/math]
. L'area di un triangolo è data dal semiprodotto di due lati per il seno dell'angolo compreso:
[math]A=1/2ab \cdot (\\sin (gamma))=1/2(50cm)(13cm)(24)/(25)=336cm^2[/math]
.
Accedi a tutti gli appunti
Tutor AI: studia meglio e in meno tempo
