Esistenza dei numeri irrazionali: Laboratorio di comprensione e accettazione attraverso l'uso della carta millimetrata

Un'attività di laboratorio per comprendere i numeri irrazionali e accettarne l'esistenza. L'attività richiede l'uso di carta millimetrata. Obiettivi: distinguere tra aspetto fisico della misurazione, aspetto algoritmico del calcolo algebrico e aspetto razionale dell'osservazione geometrica; comprendere la differenza tra l'operazione di contare e quella di misurare; osservare che gli algoritmi finiti di calcolo e, conseguentemente, l'uso della calcolatrice danno luogo a risultati approssimati.

OBIETTIVI DELL'ESPERIENZA

• cogliere il significato di numero irrazionale
• distinguere tra aspetto fisico della misurazione, aspetto algoritmico del calcolo algebrico e aspetto razionale dell'osservazione geometrica
• comprendere la differenza tra l'operazione di contare e quella di misurare
• osservare che gli algoritmi finiti di calcolo e, conseguentemente, l'uso della calcolatrice danno luogo a risultati approssimati
• constatare l'impossibilità di utilizzare la calcolatrice per operare con i numeri irrazionali
• accettare la necessità di utilizzare il calcolo con i radicali

Fase del contare

Passo 1: su un foglio di carta millimetrata disegna un quadrato di lato 10cm.

Quanti cm² misura l'area del quadrato?

Contando i quadratini all'interno si ottiene 100cm²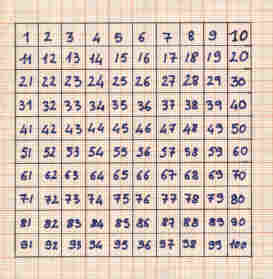

All'interno del quadrato disegna un rettangolo disposto come in figura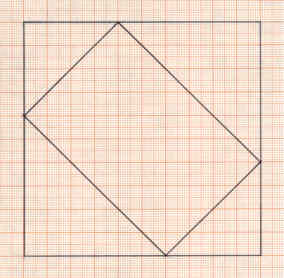

Quanti cm² misura la sua area?

Il rettangolo interno si compone di 38 quadratini interi e 20 metà quadratini, quindi 48cm²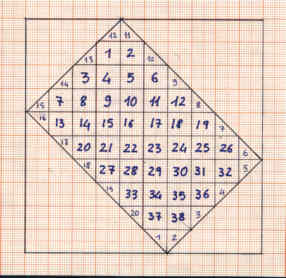

Misura con una riga la lunghezza del lato AB e del lato BC, quindi calcola l'area del rettangolo ABCD, moltiplicando le misure dei lati AB e BC.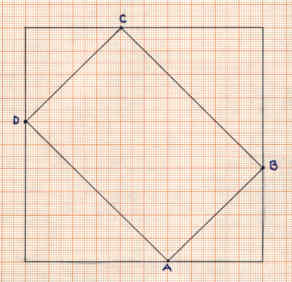

Avrai riscontrato una delle seguenti possibilità
5,5 · 8,3 = 45,65 5,5 · 8,4 = 46,20 5,5 · 8,5 = 46,75
5,5 · 8,6 = 47,30 5,6 · 8,3 = 46,48 5,6 · 8,4 = 47,04
5,6 · 8,5 = 47,60 5,6 · 8,6 = 48,16 5,7 · 8,3 = 47,31
5,7 · 8,4 = 47,88 5,7 · 8,5 = 48,45 5,7 · 8,6 = 49,02
5,8 · 8,3 = 48,14 5,8 · 8,4 = 48,72 5,8 · 8,5 = 49,30
5,8 · 8,6 = 49,88
Perché in nessun caso hai ottenuto esattamente 48?

Le misure fisiche sono sempre imprecise, prova a utilizzare il teorema di Pitagora.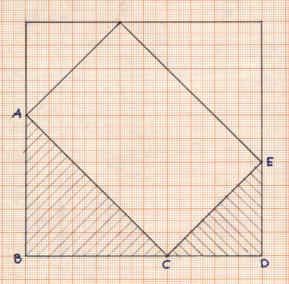

Il triangolo ABC è rettangolo. Applicando il teorema di Pitagora si ha

, da cui , analogamente . Quali misure ottieni per AC e CE?

Risposta:

, .
Osserva che utilizzando una calcolatrice a otto cifre si ha
CD = radice(32) = 5,6568542
moltiplicando AC·CD con la calcolatrice si ha 47,999999.
Proviamo a fare il calcolo con carta e penna usando il classico algoritmo della moltiplicazione. Otteniamo
8,4852813×

5,6568542=

169705626

3394112520

42426406500

678822504000

5091168780000

42426406500000

509116878000000

4242640650000000

___________________

47,99999916008646

Ancora una volta non otteniamo esattamente 48.
Dobbiamo cercare un'altro metodo

Per ottenere esattamente 48, puoi procedere in questo modo

ù

Come per magia, il numero 48 è ricomparso tutto intero.