La comodità della vita e la pratica di qualche arte [Desargues]

"Devo confessare apertamente che non ho mai avuto gusto per lo studio e per la ricerca né in geometria né in fisica se non in quanto esse potevano servirmi come mezzi per arrivare a una qualche sorta di conoscenza delle cause prossime... per il bene e la comodità della vita, nel mantenere la salute, nella pratica di qualche arte... avendo osservato che buona parte delle arti si basa sulla geometria, come fra le altre il taglio delle pietre in architettura, l'arte delle meridiane e in particolare l'arte della prospettiva.
Avendo constatato l'eccellenza e la bellezza di tali arti sono stato preso dal desiderio di capire, se mi fosse stato possibile, sia i fondamenti che le regole delle loro pratiche, quali si trovano e si vedono in uso, e ho scoperto allora che coloro che vi si dedicano ammettono di caricarsi la memoria di un gran numero di insegnamenti diversi, per ognuna di loro, che per la loro natura e condizione producono un ingombro incredibile nella loro mente e invece di aiutarli nell'esecuzione del compito, fanno loro perdere del tempo... oppure che la maggior parte dei pittori e degli altri artigiani lavorano andando alla ventura e a tentoni, senza una guida sicura, e conseguentemente con una incertezza e una fatica inimmaginabile. Il desiderio di alleviare, se possibile, alcune di queste pene, così faticose e spesso ingrate, mi ha spinto a cercare e a pubblicare per ciascuna di queste arti delle regole abbreviate... nuove, dimostrative, più facili da capire, da apprendere e da mettere in pratica."
Girarard Desargues (1591-1661), ingegnere e architetto.
Le idee di Desargues non ebbero risonanza nella comunità scientifica dell'epoca (ebbe però l'approvazione di alcuni geni della filosofia e della matematica tra cui Descartes, Fermat e Pascal che facevano parte del gruppo di matematici organizzato da padre Mersenne), ma furono invece al centro di grandi contestazioni e polemiche tra mediocri tecnici, che lo amareggiarono e stancarono tanto da farlo chiudere in una vita ritirata, a Lione, lontano dalla corte di Parigi, dedito all'insegnamento delle sue tecniche agli artigiani locali, confermando così la sua attenzione alla soluzione di problemi pratici ed applicativi (disegno in prospettiva, costruzione degli orologi, arte dei muratori, taglio delle pietre in architettura).
Il lavoro principale "Progetto di massima per studiare gli effetti dell'incontro di un cono con un piano" non fu compreso dai contemporanei anche se la sua idea era l'incarnazione della semplicità: Tutti sanno che un cerchio se guardato di sbieco, presenta l'aspetto di un 'ellisse, o che il contorno dell'ombra di un paralume sarà un cerchio o un'iperbole a seconda che sia proiettata sul soffitto o su una parete. Forme e dimensioni mutano a seconda del piano di incidenza che taglia il cono dei raggi visivi o luminosi... nell'accogliere questa concezione Desargues dovette assumere, come aveva fatto Keplero, che la parabola aveva un fuoco all'infinito e che le rette parallele si incontrano in un punto all'infinito (Vedi Carl Boyer, Storia della matematica, Oscar Mondadori).
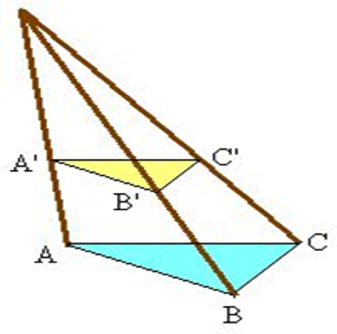
Desargues restò praticamente sconosciuto per quasi due secoli, fino a quando Poncelet, nella prima metà del XIX secolo, leggendo proprio i detrattori di Desargues, si rese pienamente conto dell'importanza di quelle idee che, da un punto di vista teorico diedero origine alla geometria proiettiva e descrittiva.
Nel linguaggio di Desargues una linea retta veniva chiamata palma. Due punti segnati su una retta erano detti tronco. Una retta contenente tre coppie di punti in involuzione era un albero. L'intento di Desargues era quello di conseguire una maggior chiarezza evitando l'ambiguità dei termini usati comunemente.
Le strane definizioni coniate da Desargues hanno lo scopo di creare un nuovo ambiente concettuale, nuove immagini mentali capaci di suggerire all'intuizione uno spazio nel quale far convivere il finito e l'infinito attuale, al fine di rimuovere gli ostacoli derivanti dalla classica visione euclidea del piano e dello spazio. In questo nuovo ambiente la mente può imparare ad orientarsi immaginando le figure dinamicamente nel loro processo di degenerazione quando una loro parte va all'infinito.