Operatori logici fondamentali

Cos come i numeri possono essere combinati attraverso le quattro operazioni aritmetiche, le proposizioni logiche possono essere combinate attraverso gli operatori logici. I principali operatori sono la negazione, la congiunzione e la disgiunzione.

Definizioni

Definizione 1: Interpretazione.
Siano date proposizioni . Una interpretazione di tali proposizioni un qualsiasi elemento di , ovvero una qualsiasi -upla costituita solo da e .

Definizione 2: Proposizione vera (o falsa) in una interpretazione.
Siano date

proposizioni ed una loro interpretazione . Per ogni , (; p_{i}) vera (o falsa) nellinterpretazione se e solo se l-esimo elemento di V (o F).

Osservazione 1: Stanti le definizioni 1 e 2, una tautologia risulta essere nullaltro che una proposizione che risulta vera in tutte le possibili interpretazioni; similmente, una contraddizione una proposizione falsa in tutte le possibili interpretazioni.

Definizione 3: Negazione.
Sia data una proposizione

. Si chiama negazione di e si indica con il simbolo (overline{p}) (che si legge non-p) la proposizione i cui valori di verit sono opposti a quelli di in tutte le possibili interpretazioni.

Osservazione 2: Se in una determinata interpretazione

la proposizione risulta vera, allora (overline{p}) falsa, e viceversa. Tutte le eventualit vengono riassunte nella tabella seguente, detta tavola di verit della negazione; in essa, ogni riga orizzontale corrisponde ad una interpretazione differente:
[
displaystyle
oxed{
egin{array}{c|c}
p&overline{p} \
hline
V&F \
F&V
end{array}
}
]

Definizione 4: Congiunzione.
Siano date due proposizioni

e . Si chiama congiunzione di e e si indica con il simbolo (che si legge p et q) la proposizione che risulta essere vera se e solo se e sono entrambe vere.

Osservazione 3: Dal momento che le proposizioni in gioco adesso sono due, per esse esistono

diverse interpretazioni: esse sono . I valori di verit assunti dalla congiunzione logica di e nelle varie interpretazioni sono riassunti dalla seguente tavola di verit della congiunzione:
[
displaystyle
oxed{
egin{array}{c|c|c}
p&q&p wedge q \
hline
V&V&V \
V&F&F \
F&V&F \
F&F&F
end{array}
}
]

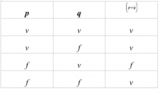
Definizione 5: Disgiunzione.

Siano date due proposizioni

e . Si chiama disgiunzione di e e si indica con il simbolo (che si legge p vel q) la proposizione che risulta essere falsa se e solo se e sono entrambe false.

Osservazione 4: Anche questa volta le proposizioni in gioco sono due, e quindi esse sono soggette alle 4 diverse interpretazioni

. I valori di verit assunti dalla disgiunzione logica di e al variare delle interpretazioni sono riassunti dalla seguente tavola di verit della disgiunzione:
[
displaystyle
oxed{
egin{array}{c|c|c}
p&q&p lor q \
hline
V&V&V \
V&F&V \
F&V&V \
F&F&F
end{array}
}
]

Esempi

Vediamo adesso quali sono i significati intuitivi dei tre operatori suddetti, attraverso alcuni esempi applicativi.
Esempio 1: Si consideri la proposizione Marco pi alto di un metro e mezzo. A che proposizione corrisponde (overline{p};)?
In questo semplice esempio, vediamo che per ottenere la negazione logica di una data proposizione sufficiente contraddire quanto da essa affermato. Ne consegue allora che (overline{p}): Laltezza di Marco minore o uguale a un metro e mezzo. Si osservi che, come atteso, vera se e soltanto se (overline{p}) falsa.

Esempio 2: Si considerino le proposizioni seguenti:

: In questo momento pi tardi delle 8.00;
: In questo momento pi presto delle 7.00.
A che proposizione corrisponde la congiunzione logica di e , cio (pwedge q;)?
In tal caso basta associare le due proposizioni con la e nel senso di e allo stesso tempo; ne risulta la proposizione In questo momento pi tardi delle 8.00 e pi presto delle 7.00. Incidentalmente, dal momento che non esiste uninterpretazione nella quale e siano vere contemporaneamente, tale proposizione sempre falsa e dunque una contraddizione.

Esempio 3: Si considerino le proposizioni seguenti:

: In questo momento pi tardi delle 7.00;
: In questo momento pi presto delle 8.00.
A che proposizione corrisponde la disgiunzione logica di e , cio (pvee q;)?
Per la disgiunzione occorre associare le due proposizioni con la o nel senso di una, oppure laltra, oppure entrambe; il risultato la proposizione In questo momento pi tardi delle 7.00 o pi presto delle 8.00. Incidentalmente, dal momento che qualsiasi orario tale da essere prima delle 8.00 oppure dopo le 7.00, non esiste alcuna interpretazione nella quale e siano false contemporaneamente; ne consegue che tale proposizione sempre vera e dunque una tautologia.

Osservazione 5: Notiamo anche, per concludere, che la negazione logica di una tautologia una contraddizione, e viceversa.