Una particolare epicicloide: la cardiode

Incominciamo disegnando due cerchi di raggio a e b tangenti esternamente con a=b .

Raggi dei cerchi:

Useremo le equazioni parametriche in funzione di per disegnare il cerchio fisso ed per quello mobile

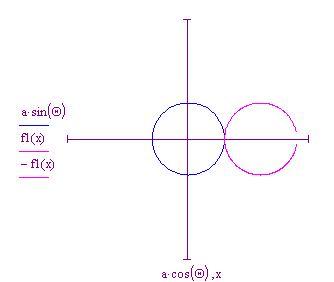
Il cerchio mobile inizia a rotolare in senso antiorario lungo la circonferenza del cerchio fisso. Se teniamo il nostro occhio fermo sul punto della circonferenza del cerchio mobile, vediamo che esso traccia una curva man mano che il cerchio rotola partendo dal punto

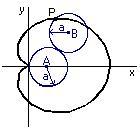
Metteremo a punto un'animazione che ci mostrerà la curva descritta dal cerchio ruotante. Con un pò di trigonometria ed il disegno qui sotto,

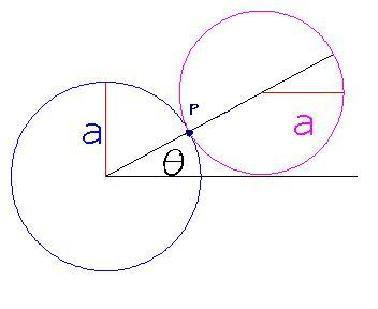
possiamo trovare le equazioni parametriche per la curva tracciata da un punto del cerchio mobile;

dove è l'angolo formato dalla linea che congiunge l'origine con il centro del cerchio mobile e l'asse . La curva sarà

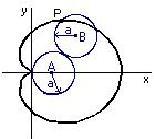
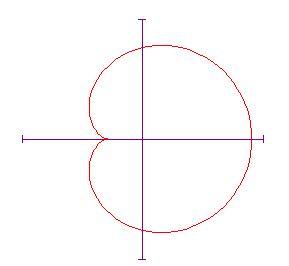
Ci piacerebbe animare il disegno della curva facendo in modo che l'angolo vari. Abbiamo bisogno di poter disegnare il cerchio rotante in qualsiasi posizione .

In tale posizione il nostro cerchio ha centro

Usando l'equazione del cerchio

Troviamo due funzioni che possono essere usate per disegnare il nostro cerchio in una posizione qualsiasi

Cambiando qui sotto, puoi vedere la nuova posizione del cerchio e la curva tracciata da esso. (Tutti gli angoli sono misurati in radianti)

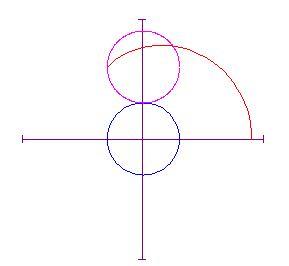
Ripetiamo l'impostazione data usando la variabile k come parametro per far variare l'angolo .

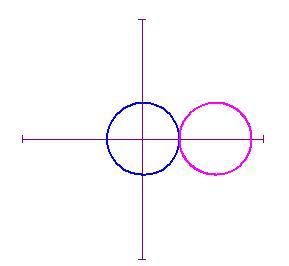
Per la Cardioide valgono le seguenti formule:

Area:

Lunghezza della curva:

Esempio : Trova l'area racchiusa dalla curva e la lunghezza della curva stessa conoscendo la lunghezza a del raggio delle circonferenze A e B

La lunghezza della curva è:

L'equazione di tale curva in coordinate polari è la seguente:

equazione in coordinate polari

Per generare la Cardioide clicca sul grafico seguente:

Cardioide