Punti medi dei lati di un triangolo - Conseguenza del Teorema di Talete
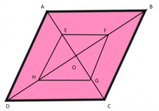
Consideriamo la seguente figura:
Corollario:
In ogni triangolo, il segmento che collega i punti medi di due lati qualsiasi, è sempre parallelo al terzo lato ed è congruente alla metà di esso.
Considerando la figura qui sopra, tradotto in simboli diventa:
[math]1) HK // BC[/math]
[math]2) BC = 2HK[/math]
Dimostrazione:Dimostriamo la prima parte della tesi:
[math]HK // BC[/math]
Sia H il punto medio di AB e K il punto medio di AC.Allora avremo che:
[math]\frac{AH}{HB} = \frac{AK}{KC} = 1[/math]
Per conseguenza inversa al Teorema di Talete, si dimostra che [math]HK // BC[/math]
.Seconda parte della tesi:
[math]BC = 2HK[/math]
Considero i triangoli AHK e ABC. Essi hanno:- HAK∠ ≅ BAC∠
- AB = 2AH
- AC = 2AK Allora, per il secondo criterio di similitudine dei triangoli, dimostriamo che:
- BC = 2HK
- AHK∠ ≅ ABC∠
- ACB∠ ≅ AKH∠ E allora si ottiene la tesi, cioè che il segmento BC è equivalente al doppio di HK.
Precisiamo che tale dimostrazione vale anche per gli altri lati, il segmento MK sarà parallelo al lato AB, mentre il segmento MH sarà parallelo al lato AC!
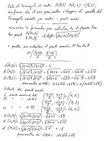
Accedi a tutti gli appunti
Tutor AI: studia meglio e in meno tempo
