Teorema dei Punti medi - Conseguenze

Teorema dei punti medi - Conseguenza

Ripetiamo l'enunciato del teorema dei punti medi, il segmento che congiunge i punti medi di due lati di un triangolo, è parallelo al terzo lato ed equivalente alla sua metà.
Conseguentemente a ciò, il triangolo che ha per vertici i punti medi dei lati di un qualsiasi triangolo, è simile al triangolo iniziale, e, equivalente ad dell'area del triangolo iniziale.
Proviamo a dimostrare
Sia un triangolo, e siano:

• D il punto medio di AB;
• E il punto medio di BC;
• F il punto medio di AC.

Per il Teorema dei Punti Medi abbiamo che:
Di conseguenza i triangoli e sono simili, perché hanno tre lati in proporzione.
Se si traccia l'altezza del triangolo e del triangolo , avremo che:
Di conseguenza il rapporto tra le aree sarà equivalente a .
Esercizio
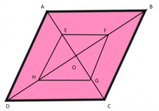
Sia ABC un triangolo equilatero di lato 8. Siano D, E, F i punti medi dei lati. Si costruisca il triangolo DEF, e si consideri il triangolo GHI dato dai punti medi dei segmenti DE, EF, DF. Calcolare l'area del triangolo GHI.
Svolgimento
Calcoliamo innanzitutto l'area del triangolo ABC.
A questo punto l'area di DEF sarà uguale a .
Infine si ottiene che l'area di GHI è uguale a: