Solidi di rotazione

I solidi di rotazione

Si definiscono "solidi di rotazione", quei particolari solidi ottenuti dalla rotazione di 360° di un poligono attorno ad una retta r. Essi sono:

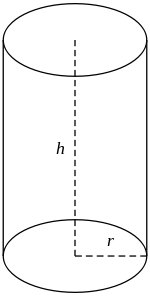
- Cilindro: è un solido di rotazione che ha origine dalla rotazione completa di un rettangolo intorno ad uno dei suoi lati. Nel caso in cui l'altezza sia congruente con il diametro della base, il cilindro si definisce equilatero. La sua superficie si calcola come:
S(t) = S(l) + 2 Ab
S(l) = 2π r h
Ab = π
[math]r^2[/math]

Mentre il suo volume si calcola come:
V = π

[math]r^2[/math]
h

- Cono: è un solido di rotazione che ha origine dalla rotazione completa di un triangolo rettangolo intorno ad uno dei suoi cateti.
La sua superficie si calcola come:
S(l) = 1/2 (2πr a) dove a rappresenta l'apotema, ovvero l'ipotenusa del triangolo che subisce la rotazione.
S(t) = S(l) + 2 Ab
Ab = π
[math]r^2[/math]

Il suo volume, invece, si calcola come:
V= 1/3 π

[math]r^2[/math]

- Sfera: la sfera è il solido di rotazione che ha origine dalla rotazione completa di una semicirconferenza intorno al suo diametro.


La sua superficie si calcola come:
S = 4π
[math]r^2[/math]
.
Mentre il suo volume si calcola come:
V = 4π/3
[math]r^2[/math]