Definizioni
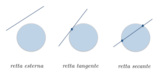
Definizione 1: Definizione di retta esterna a una circonferenzaUna retta si dice esterna a una circonferenza data se esse non hanno punti in comune.
Definizione 2: Definizione di retta tangente a una circonferenza
Una retta si dice tangente a una circonferenza data se esse hanno uno e un solo punto in comune. Tale punto è detto di tangenza.
Definizione 3: Definizione di retta secante a una circonferenza
Una retta si dice secante a una circonferenza data se esse hanno esattamente due punti in comune. Tali punti sono generalmente detti d'intersezione.

Osservazione 1: L'immagine superiore mostra tre rette nelle tre diverse posizioni che esse possono assumere rispetto alla circonferenza fissata: per la precisione, la retta ? è secante, la ? è tangente e la ? è esterna. Sono pure evidenziati i punti ?, ? d'intersezione con la retta secante e il punto ? di tangenza.
Osservazione 2: Le definizioni 1, 2 e 3 descrivono tutte le differenti posizioni nelle quali possono trovarsi una retta e una circonferenza; infatti, non è possibile che esse abbiano tre o più punti d'intersezione. Date una retta e una circonferenza generiche
[ x^2 + y^2 + alpha x + \beta y + gamma = 0 ,,, , ,,, y = mx + q ]
per trovare i punti d'intersezione occorre metterle a sistema, e calcolare
[ \begin{cases} x^2+y^2+alpha x+\beta y+gamma = 0 \ y=mx+q end{cases} Rightarrow ]
[ Rightarrow (mx+q)^2 + x^2 + alpha x + \beta(mx + q) + gamma = 0]
[ (1+m^2)x^2 + (alpha+m\beta+2mq)x+(gamma+\beta q+q^2) = 0 ]
L'equazione in
Osservazione 3: Come evidenziato nel grafico, le distanze dal centro della circonferenza di una retta ad essa secante, tangente ed esterna sono rispettivamente minore, uguale e maggiore del raggio della circonferenza stessa.
Esempi di determinazione della retta tangente
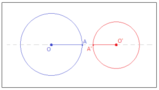
Esempio 1: Si trovino le equazioni delle rette tangenti alla circonferenza ( Gamma ) di equazione ( x^2 + y^2 + 4x - 5y + 9 ) passanti per il punto ( ABig( -frac{3}{4}, frac{5}{2} Big) ).La situazione presentata in questo esempio è la stessa che figura nell'immagine seguente:

Troviamo in primo luogo la posizione del punto ? rispetto alla circonferenza; per fare ciò prima di tutto troveremo il centro O e il raggio ?, quindi valuteremo la lunghezza di ?? e la confronteremo con il valore di ?.
( OBig(-frac{alpha}{2},-frac{\beta}{2} Big) Rightarrow OBig( -2, frac{5}{2} Big) ,,,,, r = \sqrt{frac{alpha^2}{4}+frac{\beta^2}{4}-gamma} = \sqrt{4+frac{25}{4}-9} = \sqrt{frac{5}{4}} = frac{\sqrt{5}}{2} )
( OA = \sqrt{Big(-2+frac{3}{4} Big)^2+Big( frac{5}{2}-frac{5}{2} Big)^2} = \sqrt{Big(-frac{5}{4}Big)^2} = frac{5}{4} )
( frac{5}{4} gt 1 \rightarrow frac{\sqrt{5}}{2} gt 1 \rightarrow frac{5}{2} gt \sqrt{5} \rightarrow frac{5}{4} gt frac{\sqrt{5}}{2} Rightarrow OA gt r )
Poiché ?? è più lungo del raggio della circonferenza, ? giace al di fuori di essa e quindi esisteranno due diverse rette tangenti a ( Gamma ) passanti per ?. Per trovarle, consideriamo il fascio proprio di rette centrato in ?, e intersechiamolo con ( Gamma ):
( \begin{cases} x^2+y^2+4x-5y+9 = 0 \ y-frac{5}{2} = m Big(x + frac{3}{4} Big) end{cases} Rightarrow )
( Rightarrow (m^2+1)x^2 + Big(frac{3m^2}{2}+4 Big)x + Big( frac{9m^2}{16}+frac{11}{4}Big) = 0 )
L'equazione a sinistra, ottenuta per semplice sostituzione di ?, dà le ascisse dei punti di intersezione di ogni singola retta tangente con ( Gamma ). Poiché per la definizione 2 tale punto d'intersezione deve essere uno solo, l'equazione deve avere una sola soluzione; dunque il suo ( Delta ) deve essere pari a 0.
( 0 = Delta = b^2-4ac = Big( frac{3m^2}{2} + 4 Big)^2 - 4(m^2+1)Big(frac{9m^2}{16}+frac{11}{4} Big) = 5 - frac{5m^2}{4} )
Da cui ( m = pm 2 ). Le rette tangenti si ottengono allora sostituendo nell'equazione del fascio i valori di ? trovati, avendo così
Esempio 2: Si trovino le equazioni delle rette tangenti alla circonferenza ( Gamma ) di equazione ( x^2+y^2-4x-2\sqrt{2}y+2 ) passanti per il punto ( T(2+\sqrt{2}, 2\sqrt{2}) ).
L'esempio in esame presenta la stessa situazione illustrata dall'immagine seguente:

Infatti, è facile verificare che il punto ? appartiene alla circonferenza ( Gamma ), semplicemente sostituendone le coordinate alle incognite ? e ?:
( (2+\sqrt{2})^2 + (2\sqrt{2})^2 - 4(2+\sqrt{2})-2\sqrt{2}(2\sqrt{2}) + 2 = 0 )
( 4 + 4\sqrt{2}+2 - 8 - 4 \sqrt{2} + 2 = 0 Rightarrow 0 = 0 )
Per sincerarcene avremmo anche potuto, come nell'esempio 1, trovare il centro e il raggio di ( Gamma ), quindi valutare la distanza ??: in questo caso ci saremmo accorti che ??=?. Poiché in questo caso sappiamo che ( T in Gamma ), invece che risolvere il problema in maniera algebrica con il fascio di rette come si fa di solito, potremo adoperare una soluzione più geometrica. La retta tangente a ( Gamma ) in ?, che da qui in avanti nomineremo ?, ha la proprietà di essere ortogonale alla retta passante per ? e ?; dunque per trovare ? calcoleremo in primo luogo la retta per ? e ?, quindi determineremo l'unica retta perpendicolare a questa passante per ?. Per far ciò ci occorre prima trovare ?, quindi
( OBig( -frac{alpha}{2}, -frac{\beta}{2}Big) Rightarrow O(2, \sqrt{2}) )
( r_{OT}: frac{x-2}{2+\sqrt{2}-2} = frac{y-\sqrt{2}}{2\sqrt{2}-\sqrt{2}} Rightarrow frac{x-2}{\sqrt{2}} = frac{y-\sqrt{2}}{\sqrt{2}} Rightarrow y=x+\sqrt{2} - 2 )
Infine calcoliamo ?:
( t: (y-2\sqrt{2}) = -frac{1}{m_{OT}}(x-2-\sqrt{2}) Rightarrow y=2\sqrt{2}-x+2+\sqrt{2} )
( y = -x + 2 + 3 \sqrt{2} )
Esempio 3: Si trovino le equazioni delle rette tangenti alla circonferenza ( Gamma ) di equazione ( 2x^2-3x+2y^2 = 0 ) passanti per il punto ?(?,?).
Notiamo prima di tutto che l'equazione della circonferenza non è in forma canonica; dividendo entrambi i membri per 2, avremo però
( x^2 + y^2 -frac{3}{2}x-frac{3}{2}y = 0 )
che invece è in forma canonica. Adoperiamo l'equazione ottenuta per trovare il centro e il raggio della circonferenza come facciamo sempre:
( OBig(-frac{alpha}{2},-frac{\beta}{2}Big) Rightarrow OBig(frac{3}{4},frac{3}{4}Big) ,,,,,, r=\sqrt{frac{alpha^2}{4}+frac{\beta^2}{4}-gamma} = \sqrt{frac{9}{16}+frac{9}{16}-0} = \sqrt{frac{9}{8}} = frac{3}{2\sqrt{2}} = frac{3\sqrt{2}}{4} )
In questo caso, capiamo subito che l'esercizio è impossibile perché ( OA lt r ).
( OA = \sqrt{Big(1-frac{3}{4}Big)^2+Big( 1 - frac{3}{4}Big)^2} = \sqrt{2Big(frac{1}{4}Big)^2} = \sqrt{frac{1}{8}} = frac{1}{2\sqrt{2}} = frac{\sqrt{2}}{4} lt frac{3\sqrt{2}}{4} = r )
Questo significa che il punto ? è interno alla circonferenza, e per questo motivo non può esistere alcuna retta tangente a Î passante per ?.







 Accedi a tutti gli appunti
Accedi a tutti gli appunti
 Tutor AI: studia meglio e in meno tempo
Tutor AI: studia meglio e in meno tempo