Parecchi anni fa un gruppo di ricercatori avanzò la proposta di vivere in una sfera geodesica sospesa nell'atmosfera. Questa sfera sarebbe stata trattenuta in aria mediante una differenza di temperatura tra l'interno e l'esterno della sfera in modo tale che la densità media della struttura fosse minore della densità dell'atmosfera circostante
La proposta apparve affascinante. Di seguito vengono illustrati una serie di ipotesi e calcoli che i ricercatori fecero per verificare la fattibilità di un tale modello. Non si trattava di uno studio completo, ma di un semplice progetto per vedere quali potessero essere i parametri fondamentali di una tale struttura.
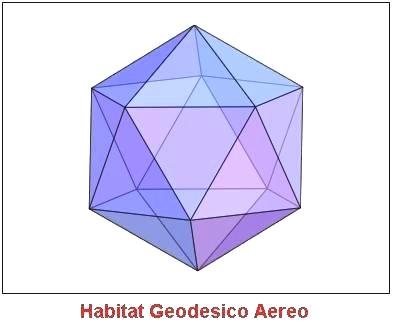
La sfera avrebbe ricevuta una spinta ascensionale poiché avrebbe avuto un'atmosfera interna meno densa dell'atmosfera esterna. La differenza di densità avrebbe compensato sia il peso dell'aria interna sia il peso della struttura geodesica. Per dimostrare come ciò potesse accadere i ricercatori considerarono le
equazioni relative al peso e alla forza ascensionale:
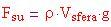

dove
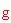
è l'accelerazione di gravità,
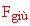
è la forza di gravità che trattiene la sfera a terra e
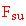
è la forza ascensionale. Il principio di
Archimede assicura che la forza verso l'alto della sfera deve essere uguale al volume della sfera (il volume dell'aria spostata) per la densità dell'aria circostante per l'accelerazione di gravità g . La sfera geodesica incomincerà a galleggiare quando
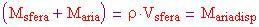
Bisogna calcolare la densità dell'aria e la massa dell'aria all'interno della sfera più la massa della sfera geodesica stessa . Incominciamo con la densità dell'aria esterna
L'Atmosfera dentro e fuori l'Aerosfera
Sarà necessario calcolare la densità media dell'atmosfera alla TPS (temperatura e pressione standard) per conoscere la densità massima della sfera galleggiante. Si assuma che l'atmosfera consista solo dei seguenti gas: ossigeno, azoto e argo e che siano presenti nelle seguenti proporzioni : 21% O 2 , 78% N 2 , e 1% Ar.
Usando la costante del volume molare e i pesi molecolari di questi tre gas, calcolare la TPS nell'atmosfera. Il volume molare di un gas ideale alla TPS è:
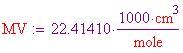
Per calcolare le densità dei tre gas più abbondanti, che compongono l'atmosfera terrestre e l'atmosfera all'interno della sfera, bisogna dividere il peso molecolare per il volume molare al fine di ottenere le densità in grammi per centimetro cubo.
Densità dell'ossigeno alla TPS:
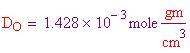
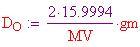
Densità dell'azoto alla TPS:
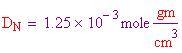
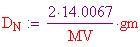
Densità dell'argo alla TPS:
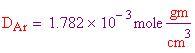
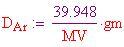
Pertanto, la densità media dell'atmosfera alla TPS è
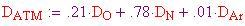
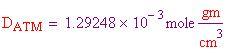
Ora si deve trovare il volume dell'aria spostata, che è pari al volume della sfera. Il volume dipende dal raggio, perciò ne prendiamo uno a caso
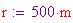
. Il volume è
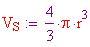
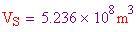
La massa d'aria spostata è
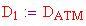
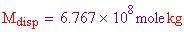
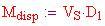
La massa della sfera
Ora che si sono stabilite le densità dei gas fuori e dentro la sfera, si deve determinare la massa della singolare sfera. Una sfera geodesica è formata da un icosaedro proiettato su una sfera. Ogni triangolo dell'icosaedro è composto da un certo numero di triangoli più piccoli. Questo dato è utile per calcolare il numero dei montanti da usare per costruire la sfera e il suo peso approssimativo.
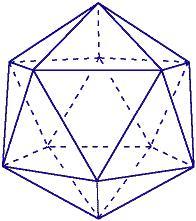
Un icosaedro: una struttura a 20 facce
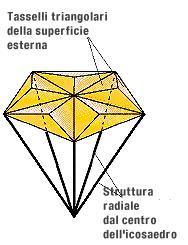
Realizzeremo i supporti interni come montanti radiali per ogni vertice dell'icosaedro tassellato. Per ottenere la lunghezza di questi raggi, prendiamo alcune sezioni della struttura e disegniamole in modo tale che sia agevole applicare i teoremi della geometria e della
trigonometria .
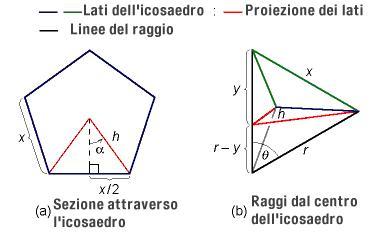
Infine ricaveremo l'angolo formato da due raggi dell'icosaedro uniti da uno stesso lato (nel diagramma è mostrato con la lettera
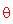
). Per fare ciò, dapprima si deve trovare la lunghezza
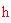
. Il seno dell'angolo
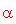
è pari al lato opposto fratto l'ipotenusa del triangolo indicato in(a) e, dato un pentagono regolare, si sa che questo angolo è pari a p-greca/5. Perciò,
Sostituiamo questo valore ad
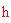
nella relazione pitagorica per il triangolo superiore nella figura (b), e troviamo la lunghezza di
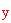
.
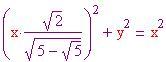
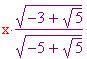
Risolvendo rispetto ad
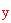
si ha come risultato
Ora si risolve l'equazione per il triangolo in basso, esplicitato in (b):
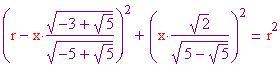
risolvendo rispetto ad
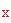
si ha come soluzione
Dalla figura (b), si sa anche che
. Sostituendo il valore di
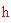
e usando il valore ricavato per
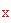
nell'espressione di
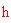
si ha
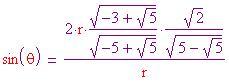
Risolvendo rispetto a
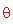
si ha
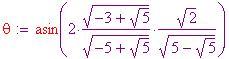
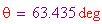
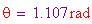
Ora occorre determinare il grado di tassellazione. Il numero di punti che suddividono ciascun lato di ciascun triangolo dell'icosaedro è
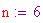
. Pertanto il numero di lati ( o meglio montanti) nella sfera geodesica è
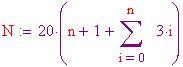
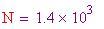
La lunghezza approssimativa di un montante della sfera geodetica, dati il raggio ed il numero di suddivisioni
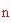
:
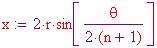
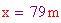
Prendiamo un'area ragionevole per la sezione di un montante:
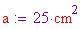
. Così, i montanti della sfera sono ognuno approssimativamente lunghi
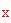
metri con una sezione di 25 cm quadrati. Potrebbero essere realizzati in un materiale leggero ma resistente, come ceramica a base di alluminio. Questo materiale ha un modulo di elasticità alto, il che significa che la struttura sarà molto rigida. E' anche abbastanza robusto (paragonato all'acciaio, al carbonio) e non molto pesante, che forse è il fattore più importante per il nostro particolare problema. La ceramica a base di allumina ha una densità di
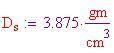
Questo ci guida alla massa approssimativa della sfera geodesica:
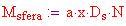
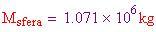
Generare una spinta
E adesso l'idea. Creeremo un gradiente termico dall'interno all'esterno della sfera riscaldando l'aria interna.
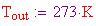
Temp. esterna:
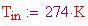
Temp. interna:
Assumeremo che la pressione interna ed esterna siano uguali, e che il volume della sfera non cambierà (da ricordare che abbiamo scelto un materiale rigido per i montanti). Ciò significa che, quando si riscalda l'interno della sfera, dovremo avere una valvola per far fuoriuscire un pò d'aria, per mantenere pressione e volume costanti mentre si sta riscaldando la temperatura. Servendoci della legge universale dei gas ideali e le nostre assunzioni su pressione e volume costante, possiamo arrivare ad una equazione per la massa dell'aria dentro la sfera, che dipende solamente dalla densità del gas esterno e dalle due temperature:
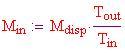
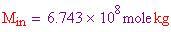
Ora si deve soddisfare l'equazione, in modo che
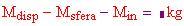
sia un numero positivo. Da un altro punto di vista, la capacità massima di spinta per la temperatura e il raggio dati è
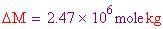
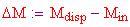
Ricordarsi che la massa della sfera era
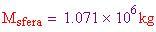
Così, in questo caso, la nostra sfera dovrebbe galleggiare abbastanza bene, e potrebbe pesare anche il doppio di quanto abbiamo stimato e continuare a galleggiare. Questo margine è importante, poiché non abbiamo preso in considerazione la pannellatura di chiusura della sfera, né il peso delle partizioni interne, gli arredi e la gente.
I parametri di ingresso per determinare se una sfera galleggerà sono il raggio
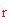
, le temperature
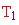
e
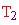
il numero di suddivisioni nell'icosaedro
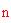
(che a sua volta determina il numero di montanti
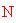
), la sezione dei montanti
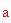
e la densità
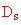
del materiale che forma i montanti, Se
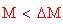
, allora la sfera galleggerà. Altrimenti si può tornare indietro e modificare uno qualsiasi dei parametri di ingresso finché non si ottiene la condizione di forza ascensionale.
Si potrebbero approfondire altre idee, come sapere a che altezza galleggerà la sfera. Se la sfera è sigillata quando viene imposta la condizione di differenziale termico, si innalzerà fino a quando la densità esterna abbia raggiunto un equilibrio con la densità interna. Ciò solleva ulteriori domande. Nell'atmosfera, la sfera esploderà se esiste un differenziale di pressione? Esistono altri materiali con cui costruire la sfera? Come si potrebbe mantenere uniforme la temperatura interna? Cosa succede se si prende in considerazione il differenziale di temperatura nell'atmosfera? Provate a dare una risposta ad alcune di queste domande per conto vostro.
 La sfera avrebbe ricevuta una spinta ascensionale poiché avrebbe avuto un'atmosfera interna meno densa dell'atmosfera esterna. La differenza di densità avrebbe compensato sia il peso dell'aria interna sia il peso della struttura geodesica. Per dimostrare come ciò potesse accadere i ricercatori considerarono le equazioni relative al peso e alla forza ascensionale:
La sfera avrebbe ricevuta una spinta ascensionale poiché avrebbe avuto un'atmosfera interna meno densa dell'atmosfera esterna. La differenza di densità avrebbe compensato sia il peso dell'aria interna sia il peso della struttura geodesica. Per dimostrare come ciò potesse accadere i ricercatori considerarono le equazioni relative al peso e alla forza ascensionale:
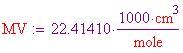 Per calcolare le densità dei tre gas più abbondanti, che compongono l'atmosfera terrestre e l'atmosfera all'interno della sfera, bisogna dividere il peso molecolare per il volume molare al fine di ottenere le densità in grammi per centimetro cubo.
Densità dell'ossigeno alla TPS:
Per calcolare le densità dei tre gas più abbondanti, che compongono l'atmosfera terrestre e l'atmosfera all'interno della sfera, bisogna dividere il peso molecolare per il volume molare al fine di ottenere le densità in grammi per centimetro cubo.
Densità dell'ossigeno alla TPS:
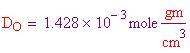
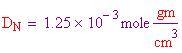
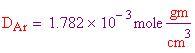
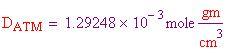 Ora si deve trovare il volume dell'aria spostata, che è pari al volume della sfera. Il volume dipende dal raggio, perciò ne prendiamo uno a caso
Ora si deve trovare il volume dell'aria spostata, che è pari al volume della sfera. Il volume dipende dal raggio, perciò ne prendiamo uno a caso  Un icosaedro: una struttura a 20 facce
Un icosaedro: una struttura a 20 facce
 Realizzeremo i supporti interni come montanti radiali per ogni vertice dell'icosaedro tassellato. Per ottenere la lunghezza di questi raggi, prendiamo alcune sezioni della struttura e disegniamole in modo tale che sia agevole applicare i teoremi della geometria e della trigonometria .
Realizzeremo i supporti interni come montanti radiali per ogni vertice dell'icosaedro tassellato. Per ottenere la lunghezza di questi raggi, prendiamo alcune sezioni della struttura e disegniamole in modo tale che sia agevole applicare i teoremi della geometria e della trigonometria .
 Infine ricaveremo l'angolo formato da due raggi dell'icosaedro uniti da uno stesso lato (nel diagramma è mostrato con la lettera
Infine ricaveremo l'angolo formato da due raggi dell'icosaedro uniti da uno stesso lato (nel diagramma è mostrato con la lettera 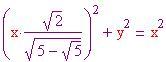
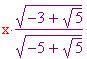 Risolvendo rispetto ad
Risolvendo rispetto ad 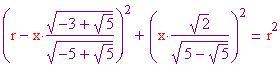 risolvendo rispetto ad
risolvendo rispetto ad 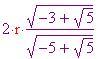 Dalla figura (b), si sa anche che
Dalla figura (b), si sa anche che 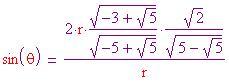 Risolvendo rispetto a
Risolvendo rispetto a 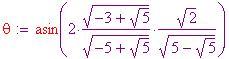
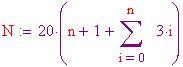
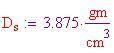 Questo ci guida alla massa approssimativa della sfera geodesica:
Questo ci guida alla massa approssimativa della sfera geodesica:
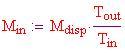







 Accedi a tutti gli appunti
Accedi a tutti gli appunti
 Tutor AI: studia meglio e in meno tempo
Tutor AI: studia meglio e in meno tempo